
分析 根据不等式的基本性质求出a,b满足的条件即可.
解答 解:∵$\root{3}{a}$+$\root{3}{b}$<$\root{3}{a+b}$,
∴${(\root{3}{a}+\root{3}{b})}^{3}$<${(\root{3}{a+b})}^{3}$,
∴a+b+3$\root{3}{{a}^{2}b}$+3$\root{3}{{ab}^{2}}$<a+b,
∴3$\root{3}{{a}^{2}b}$+3$\root{3}{{ab}^{2}}$<0,
∴a2b+ab2<0,
∴ab(a+b)<0,
∴$\left\{\begin{array}{l}{ab>0}\\{a+b<0}\end{array}\right.$或$\left\{\begin{array}{l}{ab<0}\\{a+b>0}\end{array}\right.$,
$\left\{\begin{array}{l}{a>0}\\{b<0}\\{|a|>|b|}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{b>0}\\{|b|>|a|}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{b<0}\end{array}\right.$.
点评 本题考查了不等式的基本性质,熟练掌握其性质是解题的关键,本题是一道中档题.


科目:高中数学 来源: 题型:填空题
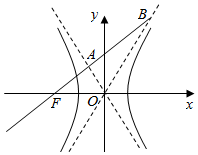 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
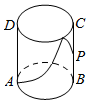 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )| A. | $\sqrt{5}$ | B. | π+1 | C. | $\sqrt{{π}^{2}+1}$ | D. | $\sqrt{{π}^{2}+9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | 8 | C. | $8\sqrt{2}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com