
| A. | 1 | B. | 0 | C. | -2 | D. | 2 |
分析 本题通过赋值法对f(2-x)=f(x)中的x进行赋值为2+x,可得-f(x)=f(2+x),可得到函数f(x)的周期为4,根据奇函数的性质得到f(0)=0,再通过赋值法得到f(1),f(2),f(3),f(4)的值,即可求解.
解答 解:∵f(2-x)=f(x),∴f[2-(2+x)]=f(2+x),即f(-x)=f(2+x),即-f(x)=f(2+x),
∴f(x+4)=f(4+x),故函数f(x)的周期为4.
∵定义在R上的奇函数f(x)满足f(2-x)-f(x)=0,且f(-1)=2,
∴f(0)=0,f(1)=-f(-1)=-2,f(2)=f(0)=0,f(3)=f(-1)=2,f(4)=f(0)=0,
∴f(1)+f(2)+f(3)+…+f(2017)=504•[f(1)+f(2)+f(3)+f(4)]+f(2017)
=504×(-2+0+2+0)+f(1)=0+(-2)=-2,
故选:C.
点评 本题通过赋值法结合奇函数的性质,利用周期性和图象平移的知识即可求解,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知唐校长某日晨练时,行走的时间(x)与离家的直线距离(y)之间的函数图象(如图).若用黑点表示唐校长家的位置,则唐校长晨练所走的路线可能是( )
已知唐校长某日晨练时,行走的时间(x)与离家的直线距离(y)之间的函数图象(如图).若用黑点表示唐校长家的位置,则唐校长晨练所走的路线可能是( )| A. |  | B. | 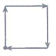 | C. |  | D. | 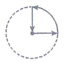 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{\frac{a}{a-1}}$ | B. | $\sqrt{5}$+1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com