
°æƒø°ø∂‘”⁄ ˝¡–{an}£¨»Ù¥”µ⁄∂˛œÓ∆µƒ√ø“ªœÓæ˘¥Û”⁄∏√œÓ÷Æ«∞µƒÀ˘”–œÓµƒ∫Õ£¨‘Ú≥∆{an}Œ™P ˝¡–.
£®1£©»Ù{an}µƒ«∞nœÓ∫ÕSn£Ω3n+2£¨ ‘≈–∂œ{an} «∑Ò «P ˝¡–£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©…Ë ˝¡–a1£¨a2£¨a3£¨°≠£¨a10 « ◊œÓŒ™©Å1°¢π´≤ÓŒ™dµƒµ»≤Ó ˝¡–£¨»Ù∏√ ˝¡– «P ˝¡–£¨«Ûdµƒ»°÷µ∑∂Œß£ª
£®3£©…ËŒÞ«Ó ˝¡–{an} « ◊œÓŒ™a°¢π´±»Œ™qµƒµ»±» ˝¡–£¨”–«Ó ˝¡–{bn}£¨{cn} «¥”{an}÷–»°≥ˆ≤ø∑÷œÓ∞¥‘≠¿¥µƒÀ≥–ÚÀ˘◊È≥…µƒ≤ªÕ¨ ˝¡–£¨∆‰À˘”–œÓ∫Õ∑÷±Œ™T1£¨T2£¨«Û{an} «P ˝¡– ±a”ÎqÀ˘¬˙◊„µƒÃıº˛£¨≤¢÷§√˜√¸Ã‚°∞»Ùa£æ0«“T1£ΩT2£¨‘Ú{an}≤ª «P ˝¡–°±.
°æ¥∞∏°ø£®1£© ˝¡–{an} «P ˝¡–£ªœÍº˚Ω‚Œˆ£®2£©![]() £®3£©
£®3£©![]() ªÚ
ªÚ £ª÷§√˜º˚Ω‚Œˆ
£ª÷§√˜º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©œ»«ÛΩ‚ ˝¡–µƒÕ®œÓπ´ Ω£¨»ª∫ÛΩ·∫œP ˝¡–µƒÃÿµ„Ω¯––—È÷§£ª
£®2£©œ»«ÛΩ‚ ˝¡–µƒÕ®œÓπ´ Ω£¨»ª∫ÛΩ·∫œP ˝¡–µƒÃÿµ„¡–≥ˆ≤ªµ»πÿœµ£¨»ª∫ÛΩ¯––«ÛΩ‚£ª
£®3£©∏˘æðP ˝¡–Ω®¡¢≤ªµ»πÿœµ£¨«ÛΩ‚≤ªµ» Ωø…µ√.
£®1£©°þ![]() £¨
£¨
°ý![]() £¨
£¨
µ±n£Ω1 ±£¨a1£ΩS1£Ω5£¨
π ![]() £¨
£¨
ƒ«√¥µ±![]() ±£¨
±£¨![]() £¨∑˚∫œÃ‚“‚£¨
£¨∑˚∫œÃ‚“‚£¨
π ˝¡–{an} «P ˝¡–.
£®2£©”…“‚÷™£¨∏√ ˝¡–µƒ«∞nœÓ∫ÕŒ™![]() £¨
£¨
”… ˝¡–a1£¨a2£¨a3£¨°≠£¨a10 «P ˝¡–£¨ø…÷™a2£æS1£Ωa1£¨π π´≤Ód£æ0£¨
![]() ∂‘¬˙◊„n£Ω1£¨2£¨3£¨
∂‘¬˙◊„n£Ω1£¨2£¨3£¨![]() £¨9µƒ»Œ“‚n∂º≥…¡¢£¨‘Ú
£¨9µƒ»Œ“‚n∂º≥…¡¢£¨‘Ú![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
π dµƒ»°÷µ∑∂ŒßŒ™![]() .
.
£®3£©¢Ÿ»Ù{an} «P ˝¡–£¨‘Úa£ΩS1£ºa2£Ωaq£¨
»Ùa£æ0£¨‘Úq£æ1£¨”÷”…an+1£æSn∂‘“ª«–’˝’˚ ˝n∂º≥…¡¢£¨ø…÷™![]() £¨º¥
£¨º¥![]() ∂‘“ª«–’˝’˚ ˝n∂º≥…¡¢£¨
∂‘“ª«–’˝’˚ ˝n∂º≥…¡¢£¨
”…![]() £¨π 2©Åq°Ð0£¨ø…µ√q°ð2£¨£ª
£¨π 2©Åq°Ð0£¨ø…µ√q°ð2£¨£ª
»Ùa£º0£¨‘Úq£º1£¨”÷”…an+1£æSn∂‘“ª«–’˝’˚ ˝n∂º≥…¡¢£¨ø…÷™![]() £¨º¥£®2©Åq£©qn£º1∂‘“ª«–’˝’˚ ˝n∂º≥…¡¢£¨
£¨º¥£®2©Åq£©qn£º1∂‘“ª«–’˝’˚ ˝n∂º≥…¡¢£¨
”÷µ±q° £®©Å°Þ£¨©Å1] ±£¨£®2©Åq£©qn£º1µ±n£Ω2 ±≤ª≥…¡¢£¨
π ”–![]() ªÚ
ªÚ![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ýµ±{an} «P ˝¡– ±£¨a”Îq¬˙◊„µƒÃıº˛Œ™![]() ªÚ
ªÚ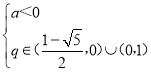 £ª
£ª
¢⁄ºŸ…Ë{an} «P ˝¡–£¨‘Ú”…¢Ÿø…÷™£¨q°ð2£¨a£æ0£¨«“{an}÷–√ø“ªœÓæ˘Œ™’˝ ˝£¨
»Ù{bn}÷–µƒ√ø“ªœÓ∂º‘⁄{cn}÷–£¨‘Ú”…’‚¡Ω ˝¡– «≤ªÕ¨ ˝¡–£¨ø…÷™T1£ºT2£ª
»Ù{cn}÷–µƒ√ø“ªœÓ∂º‘⁄{bn}÷–£¨Õ¨¿Ìø…µ√T1£æT2£ª
»Ù{bn}÷–÷¡…Ÿ”–“ªœÓ≤ª‘⁄{cn}÷–«“{cn}÷–÷¡…Ÿ”–“ªœÓ≤ª‘⁄{bn}÷–£¨
…Ë{bn'}£¨{cn' «Ω´{bn}£¨{cn}÷–µƒπ´π≤œÓ»•µÙ÷Æ∫Õ £”ýœÓ“¿¥Œππ≥…µƒ ˝¡–£¨À¸√«µƒÀ˘”–œÓ∫Õ∑÷±Œ™T1'£¨T2'£¨
≤ª∑¡…Ë{bn'}£¨{cn'}÷–◊Ó¥ÛµƒœÓ‘⁄{bn'}÷–£¨…ËŒ™am£®m°ð2£©£¨
‘ÚT2'°Ða1+a2+°≠°≠+am©Å1£ºam°ÐT1'£¨π T2'£ºT1'£¨π ◊Д–T1°ŸT2”ÎT1£ΩT2√¨∂У¨π ºŸ…˥ۣ̌¨‘≠√¸Ã‚’˝»∑.


 ∆⁄ƒ©±¶µ‰µ•‘™ºÏ≤‚∑÷¿ý∏¥œ∞æÌœµ¡–¥∞∏
∆⁄ƒ©±¶µ‰µ•‘™ºÏ≤‚∑÷¿ý∏¥œ∞æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f (x)£Ω(x£≠2)ex£´a(x£≠1)2£¨Ã÷¬€f (x)µƒµ•µ˜–‘£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë∫Ø ˝![]() .
.
£®1£©»Ù∫Ø ˝![]() ”–¡Ω∏ˆº´÷µµ„£¨«Û µ ˝
”–¡Ω∏ˆº´÷µµ„£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©…Ë![]() £¨»Ùµ±
£¨»Ùµ±![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() µƒ¡Ω∏ˆº´÷µµ„
µƒ¡Ω∏ˆº´÷µµ„![]() ¬˙◊„
¬˙◊„![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡Àπ·≥𬉠µ÷–—Î ° –πÿ”⁄–¬–Õπ⁄◊¥≤°∂æ∑Œ—◊“þ«È∑¿øÿπ§◊˜“™«Û£¨ª˝º´”¶∂‘–¬–Õπ⁄◊¥≤°∂æ“þ«È£¨«– µ◊ˆ∫√2020ƒÍ¥∫ºæø™—ßπ§◊˜£¨±£’œ–£‘∞∞≤»´Œ»∂®£¨∆’º∞∑¿øÿ÷™ ∂£¨»∑±£ ¶…˙…˙√¸∞≤»´∫Õ…ÌÃÂΩ°øµ.ƒ≥–£ø™—ß«∞£¨◊È÷Ø∏þ»˝ƒÍº∂800√˚—ß…˙≤Œº”¡À°∞“þ«È∑¿øÿ°±Õ¯¬Á÷™ ∂æ∫»¸(¬˙∑÷150∑÷).“—÷™’‚800√˚—ß…˙µƒ≥…º®æ˘≤ªµÕ”⁄90∑÷£¨Ω´’‚800√˚—ß…˙µƒ≥…º®∑÷◊È»Áœ¬£∫µ⁄“ª◊È![]() £¨µ⁄∂˛◊È
£¨µ⁄∂˛◊È![]() £¨µ⁄»˝◊È
£¨µ⁄»˝◊È![]() £¨µ⁄Àƒ◊È
£¨µ⁄Àƒ◊È![]() £¨µ⁄ŒÂ◊È
£¨µ⁄ŒÂ◊È![]() £¨µ⁄¡˘◊È
£¨µ⁄¡˘◊È![]() £¨µ√µΩµƒ∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ æ.
£¨µ√µΩµƒ∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ æ.

£®1£©«Û![]() µƒ÷µ≤¢π¿º∆’‚800√˚—ß…˙µƒ∆Ωæ˘≥…º®(Õ¨“ª◊È÷–µƒ ˝æð”√∏√◊È«¯º‰µƒ÷–µ„÷µ¥˙±Ì)£ª
µƒ÷µ≤¢π¿º∆’‚800√˚—ß…˙µƒ∆Ωæ˘≥…º®(Õ¨“ª◊È÷–µƒ ˝æð”√∏√◊È«¯º‰µƒ÷–µ„÷µ¥˙±Ì)£ª
£®2£©∏√–£°∞»∫∑¿»∫øÿ°±∂Ω≤È◊ÈŒ™∏¸∫√µÿ∂Ω¥Ÿ∏þ»˝—ß…˙µƒ°∞∏ˆ»À∑¿øÿ°±£¨◊º±∏¥”’‚800√˚—ß…˙÷–»°2√˚—ß…˙≤Œ”Î∂Ω≤Èπ§◊˜£¨∆‰»°∞Ï∑® «£∫œ»‘⁄µ⁄∂˛◊ȵ⁄ŒÂ◊ȵ⁄¡˘◊È÷–”√∑÷≤„≥È—˘µƒ∑Ω∑®≥È»°6√˚—ß…˙£¨‘Ÿ¥”’‚6√˚—ß…˙÷–Àʪ˙≥È»°2√˚—ß…˙.º«’‚2√˚—ß…˙µƒæ∫»¸≥…º®∑÷±Œ™![]()
![]() .«Û ¬º˛
.«Û ¬º˛![]() µƒ∏≈¬ .
µƒ∏≈¬ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
£®1£©»Ù∫Ø ˝![]() £¨«Û
£¨«Û![]() µƒº´÷µ£ª
µƒº´÷µ£ª
£®2£©÷§√˜£∫![]() .
.
£®≤Œøº ˝æð£∫![]()
![]()
![]()
![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷±œþ![]() …œµƒ∂ص„
…œµƒ∂ص„![]() µΩµ„
µΩµ„![]() µƒæý¿Î «À¸µΩµ„
µƒæý¿Î «À¸µΩµ„![]() µƒæý¿Îµƒ3±∂.
µƒæý¿Îµƒ3±∂.
£®1£©«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®2£©…ËÀ´«˙œþ![]() µƒ”“Ω𵄠«
µƒ”“Ω𵄠«![]() £¨À´«˙œþæ≠π˝∂ص„
£¨À´«˙œþæ≠π˝∂ص„![]() £¨«“
£¨«“![]() £¨«ÛÀ´«˙œþµƒ∑Ω≥ãª
£¨«ÛÀ´«˙œþµƒ∑Ω≥ãª
£®3£©µ„![]() πÿ”⁄÷±œþ
πÿ”⁄÷±œþ![]() µƒ∂‘≥∆µ„Œ™
µƒ∂‘≥∆µ„Œ™![]() £¨ ‘Œ ƒÐ∑Ò’“µΩ“ªÃı–±¬ Œ™
£¨ ‘Œ ƒÐ∑Ò’“µΩ“ªÃı–±¬ Œ™![]() £®
£®![]() £©µƒ÷±œþ
£©µƒ÷±œþ![]() ”Σ®2£©÷–µƒÀ´«˙œþ
”Σ®2£©÷–µƒÀ´«˙œþ![]() Ωª”⁄≤ªÕ¨µƒ¡Ωµ„
Ωª”⁄≤ªÕ¨µƒ¡Ωµ„![]() °¢
°¢![]() £¨«“¬˙◊„
£¨«“¬˙◊„![]() £¨»Ù¥Ê‘⁄£¨«Û≥ˆ–±¬
£¨»Ù¥Ê‘⁄£¨«Û≥ˆ–±¬ ![]() µƒ»°÷µ∑∂Œß£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ»°÷µ∑∂Œß£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®±æ–°Ã‚¬˙∑÷12∑÷£©“ª∏ˆ∫–◊”¿Ô◊∞”–»˝’≈ø®∆¨£¨∑÷±±Íº«”– ˝◊÷![]() £¨
£¨![]() £¨
£¨![]() £¨’‚»˝’≈ø®∆¨≥˝±Íº«µƒ ˝◊÷Õ‚ÕÍ»´œýÕ¨°£Àʪ˙”–∑≈ªÿµÿ≥È»°
£¨’‚»˝’≈ø®∆¨≥˝±Íº«µƒ ˝◊÷Õ‚ÕÍ»´œýÕ¨°£Àʪ˙”–∑≈ªÿµÿ≥È»°![]() ¥Œ£¨√ø¥Œ≥È»°
¥Œ£¨√ø¥Œ≥È»°![]() ’≈£¨Ω´≥È»°µƒø®∆¨…œµƒ ˝◊÷“¿¥Œº«Œ™
’≈£¨Ω´≥È»°µƒø®∆¨…œµƒ ˝◊÷“¿¥Œº«Œ™![]() £¨
£¨![]() £¨
£¨![]() .
.
£®¢Ò£©«Û°∞≥È»°µƒø®∆¨…œµƒ ˝◊÷¬˙◊„![]() °±µƒ∏≈¬ £ª
°±µƒ∏≈¬ £ª
£®¢Ú£©«Û°∞≥È»°µƒø®∆¨…œµƒ ˝◊÷![]() £¨
£¨![]() £¨
£¨![]() ≤ªÕÍ»´œýÕ¨°±µƒ∏≈¬ .
≤ªÕÍ»´œýÕ¨°±µƒ∏≈¬ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–![]() °¢
°¢![]() °¢
°¢![]() ¬˙◊„
¬˙◊„![]() £¨
£¨![]() £Æ
£Æ
£®1£©»Ù ˝¡–![]() «µ»±» ˝¡–£¨ ‘≈–∂œ ˝¡–
«µ»±» ˝¡–£¨ ‘≈–∂œ ˝¡–![]() «∑ÒŒ™µ»±» ˝¡–£¨≤¢Àµ√˜¿Ì”…£ª
«∑ÒŒ™µ»±» ˝¡–£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©»Ù![]() «°∫√ «“ª∏ˆµ»≤Ó ˝¡–µƒ«∞
«°∫√ «“ª∏ˆµ»≤Ó ˝¡–µƒ«∞![]() œÓ∫Õ£¨«Û÷§£∫ ˝¡–
œÓ∫Õ£¨«Û÷§£∫ ˝¡–![]() «µ»≤Ó ˝¡–£ª
«µ»≤Ó ˝¡–£ª
£®3£©»Ù ˝¡–![]() «∏˜œÓæ˘Œ™’˝ ˝µƒµ»±» ˝¡–£¨ ˝¡–
«∏˜œÓæ˘Œ™’˝ ˝µƒµ»±» ˝¡–£¨ ˝¡–![]() «µ»≤Ó ˝¡–£¨«Û÷§£∫ ˝¡–
«µ»≤Ó ˝¡–£¨«Û÷§£∫ ˝¡–![]() «µ»≤Ó ˝¡–£Æ
«µ»≤Ó ˝¡–£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™÷±œþ![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() Ωª”⁄≤ªÕ¨µƒ¡Ωµ„
Ωª”⁄≤ªÕ¨µƒ¡Ωµ„![]() £¨
£¨![]() .
.
£®1£©»Ùœþ∂Œ![]() µƒ÷–µ„Œ™
µƒ÷–µ„Œ™![]() £¨«Û÷±œþ
£¨«Û÷±œþ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©»Ù![]() µƒ–±¬ Œ™
µƒ–±¬ Œ™![]() £¨«“
£¨«“![]() π˝Õ÷‘≤
π˝Õ÷‘≤![]() µƒ◊ÛΩπµ„
µƒ◊ÛΩπµ„![]() £¨
£¨![]() µƒ¥π÷±∆Ω∑÷œþ”Î
µƒ¥π÷±∆Ω∑÷œþ”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() Œ™∂®÷µ.
Œ™∂®÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com