【题目】已知三棱锥
，从
、
、
三点及各棱中点共9个点中任取不共面4点，共______种不同的取法.（用数字作答）
【答案】90
【解析】
由题意知从9个点中任取4个点有
种取法，减去不合题意的结果，4点共面的情况有三类，取出的4个点位于四面体的同一个面上；取任一条棱上的3个点及该棱对棱的中点；由中位线构成的平行四边形，用所有的结果减去不合题意的结果即可求出答案.
从9个点中任取4个点有种取法，
其中4点共面的情况有三类.
第一类，取出的4个点位于四面体的同一个面上，有
中；
第二类，取底面BCD中任一条棱上的3个点及该棱对棱的中点，这4点共面，有3种；
第三类，由中位线构成的平行四边形（其两组对边分别平行于四面体相对的两条棱），它的4顶点共面，有3种.
以上三类情况不合要求应减掉，
所以9个点中任取不共面4点，不同的取法共有
种.
故答案为：90.
发散思维新课堂系列答案科目：高中数学 来源： 题型：
【题目】已知点
，
，
，设
，
，其中
为坐标原点.
（1）设点
在
轴上方，到线段
所在直线的距离为
，且
，求
和线段
的大小；
（2）设点
为线段
的中点，若
，且点在第二象限内,求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】P是圆
上的动点，P点在x轴上的射影是D，点M满足
．
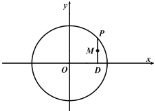
（1）求动点M的轨迹C的方程，并说明轨迹是什么图形；
（2）过点
的直线l与动点M的轨迹C交于不同的两点A，B，求以OA，OB为邻边的平行四边形OAEB的顶点E的轨迹方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
在
处的切线方程为
.
（1）求函数
的解析式；
（2）若关于
的方程f（x）＝kex（其中e为自然对数的底数）恰有两个不同的实根，求实数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知二次函数
（
、
、
均为实常数，
）的最小值是0，函数
的零点是
和
，函数
满足
，其中
，为常数.
（1）已知实数
、
满足、
，且
，试比较
与
的大小关系，并说明理由；
（2）求证：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，已知椭圆
的左顶点为
，过的直线交椭圆
于另一点
，直线
交
轴于点
，且
.
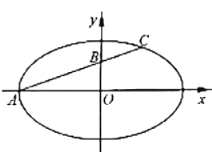
（1）求椭圆的离心率；
（2）若椭圆的焦距为
，
为椭圆上一点，线段
的垂直平分线
在轴上的截距为
（不与轴重合），求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点A是以BC为直径的圆O上异于B，C的动点，P为平面ABC外一点，且平面PBC⊥平面ABC，BC＝3，PB＝2
，PC
，则三棱锥P﹣ABC外接球的表面积为______．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面有五个命题：
①函数
的最小正周期是
；
②终边在y轴上的角的集合是
；
③在同一坐标系中，函数
的图象和函数
的图象有一个公共点；
④把函数
；
⑤在
中，若
，则是等腰三角形
；
其中真命题的序号是（ ）
A．（1）（2）（3） B．（2）（3）（4）
C．（3）（4）（5） D．（1）（4）（5）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
