【题目】下面有五个命题：
①函数
的最小正周期是
；
②终边在y轴上的角的集合是
；
③在同一坐标系中，函数
的图象和函数
的图象有一个公共点；
④把函数
；
⑤在
中，若
，则是等腰三角形
；
其中真命题的序号是（ ）
A．（1）（2）（3） B．（2）（3）（4）
C．（3）（4）（5） D．（1）（4）（5）
【答案】C
【解析】
试题化简函数的解析式求出函数的周期，可判断①的真假；写出指定角的集合，比照后可判断②的真假；在同一坐标系中画出两个函数的图象，可判断③的真假；根据函数图象的平移法则，可判断④的真假；由正弦定理及正切函数的性质，可判断⑤的真假；进而得到答案．：①函数
的最小正周期是
，故①错误；②终边在y轴上的角的集合是
}，故②错误；③在同一坐标系中，函数y=sinx的图象和函数y=x的图象有（0，0）一个公共点，故③正确；④把函数
的图象向右平移
得到
的图象，故④正确；⑤在△ABC中，若acosB=bcosA，即sinAcosB=sinBcosA，即tanA=tanB，即A=B，则△ABC是等腰三角形，故⑤正确；故选C
天天练口算系列答案科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，点
，直线
，设圆
的半径为1， 圆心在
上.
（1）若圆心也在直线
上，过点
作圆的切线，求切线方程；
（2）若圆上存在点
，使
，求圆心的横坐标
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，其图象在点
处切线的斜率为-3.
（1）求
与
关系式；
（2）求函数
的单调区间（用只含有
的式子表示）；
（3）当
时，令
，设
是函数
的两个零点， 
是
与
的等差中项，求证： 
（
为函数
的导函数）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我们知道一次函数、二次函数的图像都是连续不断的曲线，事实上，多项式函数的图像都是如此.
（1）设
，且
，若还有
，求证：
；
（2）设一个多项式函数有奇次项
（
），求证：总能通过只调整的系数，使得调整后的多项式一定有零点；
（3）现有未知数为
的多项式方程
（其中实数
待定），甲、乙两人进行一个游戏：由甲开始交替确定
中的一个数（每次只能去确定剩余还未定的数），当甲确定最后一个数后，若方程由实数解，则乙胜，反之甲胜，问：乙有必胜的策略吗？若有，请给出策略并证明，若无，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中， 
， 
， 
， 
是
中点（如图1）.将
沿
折起到图2中
的位置，得到四棱锥
.
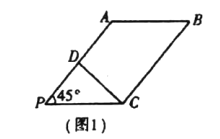
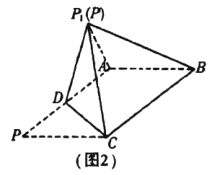
（1）将
沿
折起的过程中， 
平面
是否成立？并证明你的结论；
（2）若
与平面
所成的角为60°，且
为锐角三角形，求平面
和平面
所成角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格．某校有800 名学生参加了初赛，所有学生的成绩均在区间
内，其频率分布直方图如图所示．
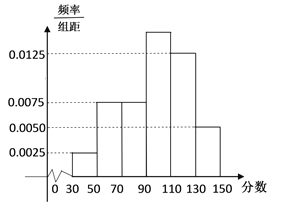
（Ⅰ）求初赛分数在区间
内的频率；
（Ⅱ）求获得复赛资格的人数；
（Ⅲ）据此直方图估算学生初赛成绩的平均数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动圆过定点
，且在y轴上截得的弦MN的长为4．
（1）求动圆圆心的轨迹C的方程；
（2）过点
的直线
与曲线C交于A、B两点，线段AB的垂直平分线与x轴交于点E（
,0），求的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有
六支足球队参加单循环比赛（即任意两支球队只踢一场比赛），第一周的比赛中
，各踢了
场， 
各踢了
场， 
踢了
场，且
队与
队未踢过， 
队与
队也未踢过，则在第一周的比赛中， 
队踢的比赛的场数是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场举行有奖促销活动，顾客购买一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球，在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖.
（1）求顾客抽奖1次能获奖的概率；
（2）若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为
，求的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com