练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知AC、BD为圆O：x2＋y2＝4的两条相互垂直的弦，垂足为M(1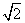，)，则四边形ABCD的面积的最大值为________．


    5

    解析：设圆心O到AC、BD的距离分别为d1、d2，垂足分别为E、F，则四边形OEMF为矩形，则有d＋d＝3.由平面几何知识知|AC|＝2，|BD|＝2，∴ S四边形ABCD＝|AC|·|BD|＝2·≤(4－d)＋(4－d)＝8－(d＋d)＝5，即四边形ABCD面积的最大值为5.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设的内角所对的边分别为且，则角      ；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    所有棱长均为2的三棱柱中，，则三棱柱的表面积为_________________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知方程x2＋y2－2(m＋3)x＋2(1－4m2)y＋16m4＋9＝0表示一个圆．

    (1) 求实数m的取值范围；

    (2) 求该圆半径r的取值范围；

    (3) 求圆心的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


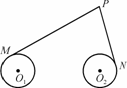
    如图，圆O1与圆O2的半径都是1，O1O2＝4，过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点)，使得PM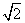＝PN，试建立适当的坐标系，并求动点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若方程ax2＋ay2－4(a－1)x＋4y＝0表示圆，求实数a的取值范围，并求出半径最小的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体A1B1C1D1—ABCD中，AC与B1D所成的角的大小为          （    ）
     
    A．    B．    C．              D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


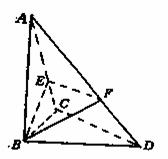
    已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且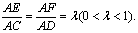

           （Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；

           （Ⅱ）(文科学生不做) 当λ为何值时，平面BEF⊥平面ACD？

                                               

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数（、为常数）.

    （1）若在和处取得极值，试求的值；

    （2）若在、上单调递增，且在上单调递减，又满足

    ＞1.求证：＞.

    查看答案和解析>>

    同步练习册答案