
【题目】对于直线![]() 与抛物线
与抛物线![]() ,若
,若![]() 与
与![]() 有且只有一个公共点且
有且只有一个公共点且![]() 与
与![]() 的对称轴不平行(或重合),则称
的对称轴不平行(或重合),则称![]() 与
与![]() 相切,直线
相切,直线![]() 叫做抛物线
叫做抛物线![]() 的切线.
的切线.
(1)已知![]() 是抛物线上一点,求证:过点
是抛物线上一点,求证:过点![]() 的
的![]() 的切线
的切线![]() 的斜率
的斜率![]() ;
;
(2)已知![]() 为
为![]() 轴下方一点,过
轴下方一点,过![]() 引抛物线的切线,切点分别为
引抛物线的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() 成等差数列;
成等差数列;
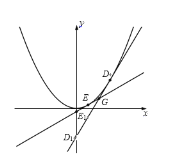
(3)如图所示,![]() 、
、![]() 是抛物线
是抛物线![]() 上异于坐标原点的两个不同的点,过点
上异于坐标原点的两个不同的点,过点![]() 的
的![]() 的切线分别是
的切线分别是![]() ,直线
,直线![]() 交于点
交于点![]() ,且与
,且与![]() 轴分别交于点
轴分别交于点![]() .设
.设![]() 为方程
为方程![]() 的两个实根,
的两个实根,![]() 表示实数
表示实数![]() 中较大的值.求证:“点
中较大的值.求证:“点![]() 在线段
在线段![]() 上”的充要条件是“
上”的充要条件是“![]() ”.
”.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析;
【解析】
(1)将抛物线方程变为![]() ,利用导数的几何意义证得结论;
,利用导数的几何意义证得结论;
(2)利用点斜式写出直线![]() ,联立可求得交点横坐标为
,联立可求得交点横坐标为![]() ,即
,即![]() ,证得结论;
,证得结论;
(3)首先联立![]() 方程,可求得
方程,可求得![]() 点坐标,进而得到
点坐标,进而得到![]() 的值;
的值;
①当![]() 在
在![]() 上时,由
上时,由![]() 可求得
可求得![]() ,进而必要性可证得;
,进而必要性可证得;
②当![]() ,可得
,可得![]() ,进而
,进而![]() ,充分性可证得;
,充分性可证得;
由此可总结出结论.
(1)将抛物线方程变为:![]()
![]()
当![]() 时,
时,![]() ,即切线
,即切线![]() 的斜率
的斜率![]()
(2)由(1)知,直线![]() ;直线
;直线![]()
由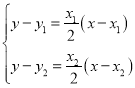 得:
得:![]()
又![]() ,
,![]()
![]()
![]()
![]()
![]() 为直线
为直线![]() 交点
交点 ![]()
![]() 成等差数列
成等差数列
(3)![]() 在抛物线上
在抛物线上 ![]()
由(1)知:![]()
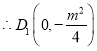
同理可得:![]()
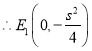
联立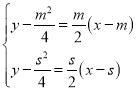 ,解得:
,解得:![]() ,
,![]() ,即
,即![]()
![]() 方程
方程![]() 两根为
两根为![]() ,
,![]()
必要性:当点![]() 在线段
在线段![]() 上时,
上时,![]()
即![]()
![]()
![]()
充分性:当![]() 时,
时,![]()
![]()
![]() ,即
,即![]()
![]() 在线段
在线段![]() 上
上
综上所述:“点![]() 在线段
在线段![]() 上”的充要条件是“
上”的充要条件是“![]() ”
”


科目:高中数学 来源: 题型:
【题目】国内某知名企业为适应发展的需要,计划加大对研发的投入,据了解,该企业原有100名技术人员,年人均投入![]() 万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员
万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员![]() 名(
名(![]() 且
且![]() ),调整后研发人员的年人均投入增加
),调整后研发人员的年人均投入增加![]() %,技术人员的年人均投入调整为
%,技术人员的年人均投入调整为![]() 万元.
万元.
(1)要使这![]() 名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
(2)是否存在这样的实数![]() ,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出
,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生,其中8名女生中有3名报考理科,男生中有2名报考文科.
(1)根据以上信息,写出![]() 列联表;
列联表;
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?
参考公式:![]()
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若整数![]() 满足:
满足:![]() ,称
,称![]() 为离实数
为离实数![]() 最近的整数,记作
最近的整数,记作![]() .给出函数
.给出函数![]() 的四个命题:
的四个命题:
①函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ;
;
②函数![]() 是周期函数,最小正周期为
是周期函数,最小正周期为![]() ;
;
③函数![]() 在
在![]() 上是增函数;
上是增函数;
④函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
其中所有的正确命题的序号为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,过点
的右焦点为F,过点![]() 的直线l与E交于A,B两点.当l过点F时,直线l的斜率为
的直线l与E交于A,B两点.当l过点F时,直线l的斜率为![]() ,当l的斜率不存在时,
,当l的斜率不存在时,![]() .
.
(1)求椭圆E的方程.
(2)以AB为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com