【题目】某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生，其中8名女生中有3名报考理科，男生中有2名报考文科.
（1）根据以上信息，写出
列联表；
（2）用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关？
参考公式：
p（K2≥k0） | 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
k0 | 2．07 | 2．71 | 3．84 | 5．02 | 6．64 | 7．88 | 10．83 |
科目：高中数学 来源： 题型：
【题目】若无穷数列
满足：
，当
'，
时，
（其中
表示
，
，…，
中的最大项），有以下结论：
① 若数列是常数列，则
；
② 若数列是公差
的等差数列，则
；
③ 若数列是公比为
的等比数列，则
：
④ 若存在正整数
，对任意，都有
，则，是数列的最大项.
其中正确结论的序号是____（写出所有正确结论的序号）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地建一座桥，两端的桥墩已建好，这两墩相距m米，余下工程只需建两端桥墩之间的桥面和桥墩．经测算，一个桥墩的工程费用为256万元；距离为x米的相邻两墩之间的桥面工程费用为(2＋
)x万元．假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素，记余下工程的费用为y万元．
(1)试写出y关于x的函数关系式；
(2)当m＝640米时，需新建多少个桥墩才能使y最小？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列
满足：
，
（其中
为非零实常数）.
（1）设
，求证：数列是等差数列，并求出通项公式；
（2）设
，记
，求使得不等式
成立的最小正整数
；
（3）若
，对于任意的正整数
，均有
，当
、
、
依次成等比数列时，求、
、
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直角梯形
的下底与等腰直角三角形
的斜边重合，
且
（如图（1）所示），将此图形沿
折叠成直二面角，连接
，
，得到四棱锥
（如图（2）所示）.
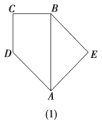
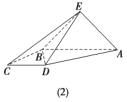
（1）线段
上是否存在点
，使
平面
？若存在，求出
；若不存在，说明理由；
（2）在（1）的条件下，求平面与平面的夹角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图已知椭圆的焦点在
轴上，其离心率为
，点
在椭圆上.
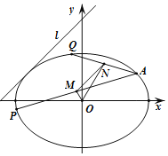
（1）求椭圆的标准方程；
（2）椭圆的弦
，
的中点分别为
，
，若
平行于
，直线与椭圆相切，且斜率为1，则
，
斜率之和是否为定值？若是定值，请求出该定值；若不是定值请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于直线
与抛物线
，若与
有且只有一个公共点且与的对称轴不平行（或重合），则称与相切，直线叫做抛物线的切线．
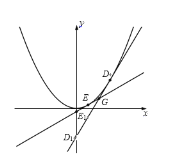
（1）已知
是抛物线上一点，求证：过点
的的切线的斜率
；
（2）已知
为
轴下方一点，过
引抛物线的切线，切点分别为
，
．求证：
成等差数列；
（3）如图所示，
、
是抛物线上异于坐标原点的两个不同的点，过点
的的切线分别是
，直线交于点
，且与
轴分别交于点
．设
为方程
的两个实根，
表示实数
中较大的值．求证：“点
在线段
上”的充要条件是“
”．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】语文成绩服从正态分布
，数学成绩的频率分布直方图如图：
（1）如果成绩大于135的为特别优秀，这500名学生中本次考试语文、数学特别优秀的大约各多少人？
（2）如果语文和数学两科都特别优秀的共有6人，从（1）中的这些同学中随机抽取3人，设三人中两科都特别优秀的有
人，求的分布列和数学期望.
（3）根据以上数据，是否有99%的把握认为语文特别优秀的同学，数学也特别优秀.
①若
，则
，
.
②
③
| 0.050 | 0.040 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
