
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ',
',![]() 时,
时,![]()
![]() (其中
(其中![]() 表示
表示![]() ,
,![]() ,…,
,…,![]() 中的最大项),有以下结论:
中的最大项),有以下结论:
① 若数列![]() 是常数列,则
是常数列,则![]() ;
;
② 若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
③ 若数列![]() 是公比为
是公比为![]() 的等比数列,则
的等比数列,则![]() :
:
④ 若存在正整数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则
,则![]() ,是数列
,是数列![]() 的最大项.
的最大项.
其中正确结论的序号是____(写出所有正确结论的序号).
【答案】①②③④
【解析】
①令n=2,![]() =
=![]() ,若数列
,若数列![]() 是常数列,则
是常数列,则![]() ,所以
,所以![]() ,即得
,即得![]() ;②若数列
;②若数列![]() 是等差数列,则
是等差数列,则![]() =max{
=max{![]() ,
,![]() ,…,
,…,![]() }=|d|,
}=|d|,![]() 有最大值,只能递减;③若数列
有最大值,只能递减;③若数列![]() 是等比数列,令n=2,
是等比数列,令n=2,![]() =
=![]() ,所以
,所以![]() 或
或![]() (舍);④
(舍);④![]() ,为周期数列,可先假设
,为周期数列,可先假设![]() 最大,由
最大,由![]() 易证得
易证得![]() ,所以
,所以![]() 最大.
最大.
解:①若数列![]() 是常数列,则
是常数列,则![]() =max{
=max{![]() ,
,![]() ,…,
,…,![]() }=0,所以
}=0,所以![]() (
(![]() ),①正确;
),①正确;
②若数列![]() 是公差d≠0的等差数列,则
是公差d≠0的等差数列,则![]() =max{
=max{![]() ,
,![]() ,…,
,…,![]() }=|d|,所以
}=|d|,所以![]() 有最大值,因此
有最大值,因此![]() 不可能递增且d≠0,所以d<0,②正确;
不可能递增且d≠0,所以d<0,②正确;
③若数列![]() 是公比为q的等比数列,则
是公比为q的等比数列,则![]() ,且
,且![]() =
=![]() =
=![]() ,所以
,所以![]() ,所以
,所以![]() 或
或![]() ,又因为
,又因为![]() ,所以
,所以![]() ,所以q>1,③正确;
,所以q>1,③正确;
④若存在正整数T,对任意![]() ,都有
,都有![]() ,假设在
,假设在![]() 中
中![]() 最大,则
最大,则![]() 中都是
中都是![]() 最大,则
最大,则![]() =
=![]() ,且
,且![]() ,即
,即![]() =
=![]() ,所以
,所以![]() ,所以
,所以![]() 是数列
是数列![]() 的最大项,④正确.
的最大项,④正确.
故答案为:①②③④.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
(1)以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,求曲线
轴的非负半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和点
的极坐标方程和点![]() 的极坐标;
的极坐标;
(2)若点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交![]() 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为![]() 元时,一年的销售量为
元时,一年的销售量为![]() 万件.
万件.
(1)求该连锁分店一年的利润![]() (万元)与每件商品的售价
(万元)与每件商品的售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)集合![]() ,
,![]() 或
或![]() ,对于任意
,对于任意![]() ,定义
,定义![]() ,对任意
,对任意![]() ,定义
,定义![]() ,记
,记![]() 为集合
为集合![]() 的元素个数,求
的元素个数,求![]() 的值;
的值;
(2)在等差数列![]() 和等比数列
和等比数列![]() 中,
中,![]() ,
,![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中,若存在,求出所有的
中,若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)已知当![]() 时,有
时,有![]() ,根据此信息,若对任意
,根据此信息,若对任意![]() ,都有
,都有![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图,直线![]() 是抛物线
是抛物线![]() (
(![]() )和圆C:
)和圆C:![]() 的公切线,切点(在第一象限)分别为P、Q.F为抛物线的焦点,切线
的公切线,切点(在第一象限)分别为P、Q.F为抛物线的焦点,切线![]() 交抛物线的准线于A,且
交抛物线的准线于A,且![]() .
.
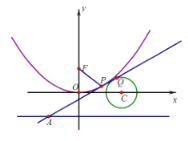
(1)求切线![]() 的方程;
的方程;
(2)求抛物线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com