
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
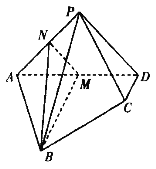
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为x轴,其准线过点![]() .
.
(1)求抛物线C的方程;
(2)过抛物线焦点F作直线l,使得抛物线C上恰有三个点到直线l的距离都为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)若![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的值;
的值;
(3)若![]() ,若当
,若当![]() 时,总有
时,总有![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名企业为适应发展的需要,计划加大对研发的投入,据了解,该企业原有100名技术人员,年人均投入![]() 万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员
万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员![]() 名(
名(![]() 且
且![]() ),调整后研发人员的年人均投入增加
),调整后研发人员的年人均投入增加![]() %,技术人员的年人均投入调整为
%,技术人员的年人均投入调整为![]() 万元.
万元.
(1)要使这![]() 名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
(2)是否存在这样的实数![]() ,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出
,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市有相交于点O的一条东西走向的公路l,与南北走向的公路m,这两条公路都与一块半径为1(单位:千米)的圆形商城A相切.根据市民建议,欲再新建一条公路PQ,点P、Q分别在公路l、m上,且要求PQ与圆形商城A也相切.
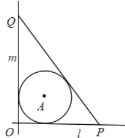
(1)当P距O处4千米时,求OQ的长;
(2)当公路PQ长最短时,求OQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由A,B,C,…等7人担任班级的7个班委.
(1)若正、副班长两职只能由A,B,C这三人中选两人担任,则有多少种分工方案?
(2)若正、副班长两职至少要选A,B,C这三人中的1人担任,有多少种分工方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生,其中8名女生中有3名报考理科,男生中有2名报考文科.
(1)根据以上信息,写出![]() 列联表;
列联表;
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?
参考公式:![]()
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com