解:(Ⅰ)f′(x)=e
x+4x-3,(1分)
令h(x)=f'(x)=e
x+4x-3,则h′(x)=e
x+4>0,(2分)
∴f′(x)在区间[0,1]上单调递增,
∵f′(0)=e
0-3=-2<0,f'(1)=e+1>0,
∴f′(0)•f′(1)<0.(3分)
又∵f′(x)在区间[0,1]上是单调函数
∴f′(x)在区间[0,1]上存在唯一零点,
∴f(x)在区间[0,1]上存在唯一的极小值点.(4分)
取区间[0,1]作为起始区间,用二分法逐次计算如下:
①f'(0.5)≈0.6>0,而f'(0)=-2<0,
∴f'(0.5)×f'(0)<0)
∴极值点所在区间是[0,0.5];
②又f'(0.3)≈-0.5<0,
∴f'(0.3)×f'(0.5)<0,
∴极值点所在区间是[0.3,0.5];
③∵|0.5-0.3|=0.2,
∴区间[0.3,0.5]内任意一点即为所求.
∴x=0.4(7分)
(Ⅱ)由

,得
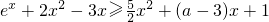
,
即

,
∵

,∴
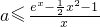
,(8分)
令
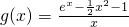
,则
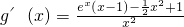
.(10分)
令
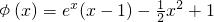
,则φ'(x)=x(e
x-1).
∵

,∴φ′(x)>0,∴φ(x)在
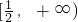
上单调递增,
∴
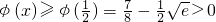
,
因此g′(x)>0,故g(x)在
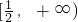
上单调递增,(12分)
则
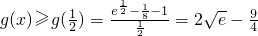
,
∴a的取值范围是
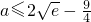
.(14分)
分析:(Ⅰ)先求函数的导数,求导数在0和1处的值,乘积小于0即可
(Ⅱ)利用分参法把a分离出来,构造函数,求函数的导数,判断函数的单调性,求a的取值范围
点评:该题考查函数的求导,判断函数的单调性,会使用二分法和分参法的方法求出a的取值范围.注意极值点的取值区间.

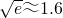 ,e0.3≈1.3)
,e0.3≈1.3) 时,若关于x的不等式
时,若关于x的不等式 恒成立,试求实数a的取值范围.
恒成立,试求实数a的取值范围. ,得
,得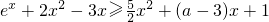 ,
, ,
, ,∴
,∴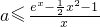 ,(8分)
,(8分)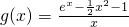 ,则
,则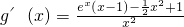 .(10分)
.(10分)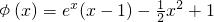 ,则φ'(x)=x(ex-1).
,则φ'(x)=x(ex-1). ,∴φ′(x)>0,∴φ(x)在
,∴φ′(x)>0,∴φ(x)在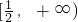 上单调递增,
上单调递增,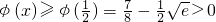 ,
,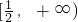 上单调递增,(12分)
上单调递增,(12分)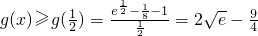 ,
,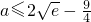 .(14分)
.(14分)
