
已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f′(n)的最小值是________.
科目:高中数学 来源:2015届高考苏教数学(理)训练4 函数及其表示(解析版) 题型:填空题
若函数f(x)=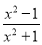 ,则
,则
(1)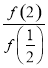 =________.
=________.
(2)f(3)+f(4)+…+f(2 012)+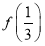 +
+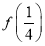 +…+
+…+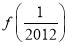 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:解答题
一个扇形OAB的面积是1 cm2,它的周长是4 cm,求圆心角的弧度数和弦长AB.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:填空题
已知函数f(x)=ln x+2x,若f(x2+2)<f(3x),则实数x的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:解答题
设函数f(x)=ln x-ax,g(x)=ex-ax,其中a为实数.若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:解答题
已知函数f(x)=x+sin x.
(1)设P,Q是函数f(x)图像上相异的两点,证明:直线PQ的斜率大于0;
(2)求实数a的取值范围,使不等式f(x)≥axcos x在 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练11 函数与方程(解析版) 题型:填空题
用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算f(0)<0,f(0.5)>0可得其中一个零点x0∈________,第二次应计算________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
若命题“?x∈R,使得x2+(a-1)x+1≤0”为假命题,则实数a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com