
分析 (1)由题意$\left\{\begin{array}{l}{{x}_{0}+\frac{p}{2}=\frac{5}{4}}\\{2p{x}_{0}=1}\end{array}\right.$,解得即可求出p的值,写出抛物线的方程即可;
(2)先求出直线MF的方程为4x+3y-4=0,联立方程得方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{4x+3y-4=0}\end{array}\right.$,求出x,y的值,由由焦半径公式|MF|=$\frac{1}{4}$+1=$\frac{5}{4}$,|NF|=4+1=5,问题得以解决.
解答 解:(1)由题意$\left\{\begin{array}{l}{{x}_{0}+\frac{p}{2}=\frac{5}{4}}\\{2p{x}_{0}=1}\end{array}\right.$,消去x0得2p2-5p+2=0,因为1<p<3,解得p=2,
所以x0=$\frac{1}{4}$,所以抛物线标准方程为y2=4x.
(2)因为F(1,0),M($\frac{1}{4}$,1),所以kMF=-$\frac{4}{3}$,直线MF的方程为4x+3y-4=0,
联立方程得方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{4x+3y-4=0}\end{array}\right.$,消去x得y2+3y-4=0,解得y=-4或1,将y=-4代入y2=4x,解得x=4,
由焦半径公式|MF|=$\frac{1}{4}$+1=$\frac{5}{4}$,|NF|=4+1=5,
所以$\frac{|MF|}{|NF|}$=$\frac{\frac{5}{4}}{5}$=$\frac{1}{4}$.
点评 本题考查了抛物线的标准方程,焦半径公式,方程组的解法,培养了学生的运算能力和转化能力,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 不合格 |
| 男生(人) | 15 | x | 5 |
| 女生(人) | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2>k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=$\sqrt{2}$,M为线段B1D1的中点.
如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=$\sqrt{2}$,M为线段B1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
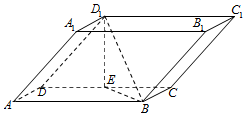 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{17}$ | B. | $\sqrt{13}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
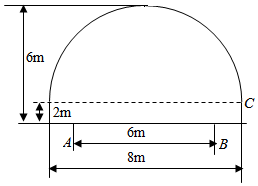 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com