练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
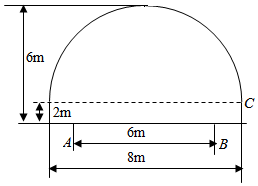
    5．如图所示，一隧道内设双行线公路，其截面由一个长方形和抛物线构成．为保证安全，要求行使车辆顶部（设为平顶）与隧道顶部在竖直方向上的高度之差至少要有0.5米．若行车道总宽度AB为6米，则车辆通过隧道的限制高度是3.2米（精确到0.1米）

    分析 先求出抛物线的解析式，再根据题意判断该隧道能通过的车辆的最高高度即可得到结论．先求出抛物线的解析式，再根据题意判断该隧道能通过的车辆的最高高度即可得到结论．

    解答 解：取抛物线的顶点为原点，对称轴为y轴，建立直角坐标系，c（4，-4），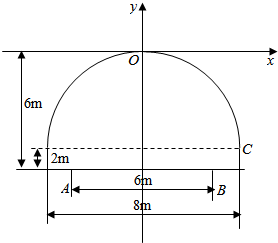
    设抛物线方程x2=-2py（p＞0），将点C代入抛物线方程得p=2，
    ∴抛物线方程为x2=-4y，行车道总宽度AB=6m，
    ∴将x=3代入抛物线方程，y=-2.25m，
    ∴限度为6-2.25-0.5=3.25m，
    ∴则车辆通过隧道的限制高度是3.2米（精确到0.1米），
    故答案为：3.2．

    点评 本题主要考查了二次函数的实际应用，解答二次函数的应用问题时，要注意自变量的取值范围还必须使实际问题有意义，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．${∫}_{0}^{1}$（3x2-$\frac{1}{2}$）dx的值是$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

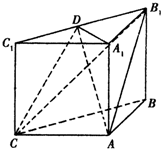    16．如图，三棱柱$ABC-A_1^{\;}B_1^{\;}C_1^{\;}$中，$A_1^{\;}A⊥底面ABC$，$AC=AB=AA_1^{\;}=4$，∠BAC=90°，点D是棱$B_1^{\;}C_1^{\;}$的中点．
    （Ⅰ）求证：$A_1^{\;}D⊥$平面$BB_1^{\;}C_1^{\;}C$；
    （Ⅱ）求三棱锥$C_1^{\;}-ADC$的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．用数学归纳法证明不等$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{2n}$＞$\frac{23}{24}$（n≥2）的过程中，由n=k递推到n=k+1时，不等式左边（　　）
    A．增加了一项$\frac{1}{2（k+1）}$B．增加了一项$\frac{1}{2k+1}+\frac{1}{2（k+1）}$
    C．增加了$\frac{1}{2k+1}+\frac{1}{2（k+1）}$，又减少了$\frac{1}{k+1}$D．增加了 $\frac{1}{2（k+1）}$，又减少了$\frac{1}{k+1}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知抛物线y2=2px（1＜p＜3）的焦点为F，抛物线上的点M（x0，1）到准线的距离为$\frac{5}{4}$
    （1）求抛物线的标准方程；
    （2）设直线MF与抛物线的另一交点为N，求$\frac{|MF|}{|NF|}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设A、B是焦点为F（1，0）的抛物线y2=2px（p＞0）上异于坐标原点的两点，若$\overrightarrow{OA}$?$\overrightarrow{OB}$=0，则坐标原点O（0，0）到直线AB距离的最大值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

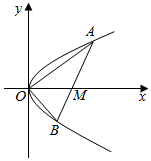    17．如图，已知直线l与抛物线y2=2px相交于A（x1，y1），B（x2，y2）两点，与x轴相交于点M（1，0）线段AB中点坐标（2，1）
    （1）求抛物线方程；
    （2）求△AOB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图，点F（0，2）是抛物线x2=2py的焦点．
    （Ⅰ）求抛物线方程；
    （Ⅱ）若点P为圆O：x2+y2=1上一动点，直线l是圆O在点P处的切线，直线l与抛物线相交于A，B 两点（A，B在y轴的两侧），求四边形OAFB的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设n＞1且n∈N+，求证：$\frac{1}{2}＜\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}＜1$．

    查看答案和解析>>

    同步练习册答案