
 如图,点F(0,2)是抛物线x2=2py的焦点.
如图,点F(0,2)是抛物线x2=2py的焦点.分析 (Ⅰ)利用点F(0,2)是抛物线x2=2py的焦点,求出p=4,即可得到抛物线方程.
(Ⅱ)设直线AB:y=kx+b,利用直线与圆相切,得到b2=1+k2,联立$\left\{{\begin{array}{l}{y=kx+b}\\{{x^2}=8y}\end{array}}\right.$消去y,设A(x1,y1),B(x2,y2)由韦达定理求出x1+x2=8k,x1•x2=-8b,表示四边形OAFB的面积,通过b的范围,求解SOAFB的最小值.
解答 解:(Ⅰ)点F(0,2)是抛物线x2=2py的焦点,可得p=4,抛物线方程为:x2=8y….(5分)
(Ⅱ)设直线AB:y=kx+b
由直线与圆相切得:$\frac{|b|}{{\sqrt{1+{k^2}}}}=1$,即b2=1+k2…①….(7分)
$\left\{{\begin{array}{l}{y=kx+b}\\{{x^2}=8y}\end{array}}\right.$化简整理得:x2-8kx-8b=0
设A(x1,y1),B(x2,y2)则x1+x2=8k,x1•x2=-8b….(9分)
∵A,B在y轴两侧,
∴x1•x2<0即b>0…②
由①②得b≥1${S_{OAFB}}=\frac{1}{2}×OF×|{x_1}|+\frac{1}{2}×OF×|{x_2}|$….(11分)
=|x1-x2|=$\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}$=$\sqrt{64{k^2}+32b}=4\sqrt{4{b^2}+2b-4}(b≥1)$….(13分)
当b=1时,SOAFB的最小值为$4\sqrt{2}$….(15分)
点评 本题考查抛物线的简单性质以及直线与抛物线的位置关系的综合应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
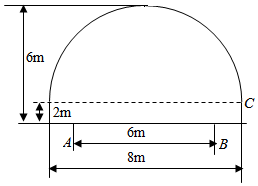 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{2}$ | B. | $\frac{3}{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 36 | C. | $\frac{31}{8}$ | D. | $\frac{63}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com