
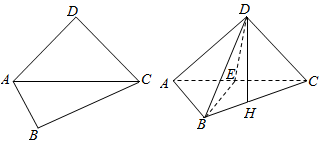
分析 (1)由DH⊥平面ABC得DH⊥AB,又AB⊥BC,故而AB⊥平面BCD;
(2)由AB⊥平面BCD得AB⊥CD,又CD⊥AD,故而CD⊥平面ABD;
(3)连结EH,则可证明AC⊥EH,根据直角三角形的性质求出DE,AE,AB,EH,利用勾股定理计算DH,代入棱锥的体积公式求出体积.
解答 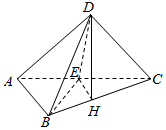 证明:(1)∵DH⊥平面ABC,AB?平面ABC,
证明:(1)∵DH⊥平面ABC,AB?平面ABC,
∴DH⊥AB,
又AB⊥BC,BC?平面BCD,DH?平面BCD,BC∩DH=H,
∴AB⊥平面BCD.
(2)∵AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD,又AD⊥CD,AD?平面ABD,AB?平面ABD,AB∩AD=A,
∴CD⊥平面ABD.
(3)∵AD=CD=$\sqrt{6}$,AD⊥CD,E是AC的中点,
∴DE⊥AC,AC=$\sqrt{2}$AD=2$\sqrt{3}$,DE=CE=AE=$\frac{1}{2}$AC=$\sqrt{3}$,
∵∠BAC=60°,∠ABC=90°,
∴AB=$\frac{1}{2}AC=\sqrt{3}$,BC=3.
连结EH,
∵DH⊥AC,DH∩DE=D,
∴AC⊥平面DEH,∴AC⊥EH.
∴△CEH∽△CBA,
∴$\frac{EH}{AB}=\frac{CE}{BC}$,即$\frac{EH}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,解得EH=1.
∴DH=$\sqrt{D{E}^{2}-E{H}^{2}}$=$\sqrt{2}$.
∴VD-ABE=$\frac{1}{3}{S}_{△ABE}•DH$=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×\sqrt{3}×sin60°×\sqrt{2}$=$\frac{\sqrt{6}}{4}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
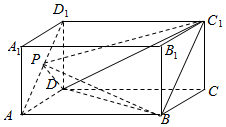 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P为线段AD1上的动点,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P为线段AD1上的动点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
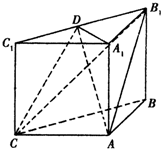 如图,三棱柱$ABC-A_1^{\;}B_1^{\;}C_1^{\;}$中,$A_1^{\;}A⊥底面ABC$,$AC=AB=AA_1^{\;}=4$,∠BAC=90°,点D是棱$B_1^{\;}C_1^{\;}$的中点.
如图,三棱柱$ABC-A_1^{\;}B_1^{\;}C_1^{\;}$中,$A_1^{\;}A⊥底面ABC$,$AC=AB=AA_1^{\;}=4$,∠BAC=90°,点D是棱$B_1^{\;}C_1^{\;}$的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加了一项$\frac{1}{2(k+1)}$ | B. | 增加了一项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$ | ||
| C. | 增加了$\frac{1}{2k+1}+\frac{1}{2(k+1)}$,又减少了$\frac{1}{k+1}$ | D. | 增加了 $\frac{1}{2(k+1)}$,又减少了$\frac{1}{k+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点F(0,2)是抛物线x2=2py的焦点.
如图,点F(0,2)是抛物线x2=2py的焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com