
| A. | 增加了一项$\frac{1}{2(k+1)}$ | B. | 增加了一项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$ | ||
| C. | 增加了$\frac{1}{2k+1}+\frac{1}{2(k+1)}$,又减少了$\frac{1}{k+1}$ | D. | 增加了 $\frac{1}{2(k+1)}$,又减少了$\frac{1}{k+1}$ |
分析 当n=k时,写出左端,并当n=k+1时,写出左端,两者比较,关键是最后一项和增加的第一项的关系.
解答 解:当n=k时,左端$\frac{1}{k+1}$+$\frac{1}{k+2}$+…+$\frac{1}{2k}$,
那么当n=k+1时 左端=$\frac{1}{k+2}$+$\frac{1}{k+3}$…+$\frac{1}{2k}$+$\frac{1}{2k+1}$+$\frac{1}{2k+2}$,
故第二步由k到k+1时不等式左端的变化是增加了$\frac{1}{2k+1}$和$\frac{1}{2k+2}$两项,同时减少了$\frac{1}{k+1}$这一项,
故选:C.
点评 本题是基础题,考查数学归纳法的证明方法,就是n=k到n=k+1时的证明方法,找出规律解答.


科目:高中数学 来源: 题型:选择题
| A. | (22015+24031)2016 | B. | 22015+24031 | C. | 2016(22015+24031) | D. | 2016(22016+24032) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
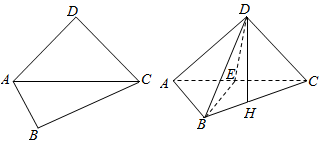
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
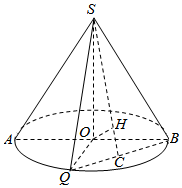 如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
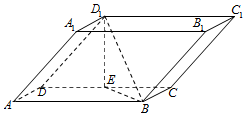 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
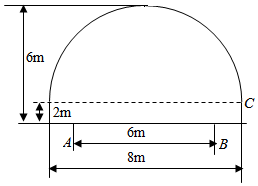 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{2}$ | B. | $\frac{3}{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com