
分析 根据题意算出抛物线的焦点为F(0,3),设M(x,y)、P的坐标为(t,$\frac{1}{12}$t2),由$\overrightarrow{FM}=\overrightarrow{MP}$,建立关于x、y、t的方程组,再消去参数t即可得到动点M的轨迹方程.
解答 解:设M的坐标为(x,y),P的坐标为(t,$\frac{1}{12}$t2)
∵抛物线y2=12y中,2p=12,可得p=6,
∴抛物线的焦点为F(0,3),
∴$\overrightarrow{FM}$=(x,y-3),$\overrightarrow{MP}$=(t-x,$\frac{1}{12}$t2-y),
又∵动点M满足$\overrightarrow{FM}=\overrightarrow{MP}$,
∴(x,y-3)=(t-x,$\frac{1}{12}$t2-y),
可得$\left\{\begin{array}{l}{x=t-x}\\{y-3=\frac{1}{12}{t}^{2}-y}\end{array}\right.$,消去参数t可得x2=6y-9,即为动点M的轨迹方程.
故答案为:x2=6y-9
点评 本题考查了求点的轨迹方程.着重考查了向量的坐标运算、抛物线的标准方程与简单几何性质等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
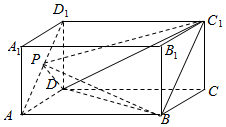 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P为线段AD1上的动点,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P为线段AD1上的动点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
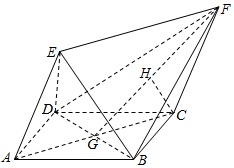 如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.
如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加了一项$\frac{1}{2(k+1)}$ | B. | 增加了一项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$ | ||
| C. | 增加了$\frac{1}{2k+1}+\frac{1}{2(k+1)}$,又减少了$\frac{1}{k+1}$ | D. | 增加了 $\frac{1}{2(k+1)}$,又减少了$\frac{1}{k+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com