
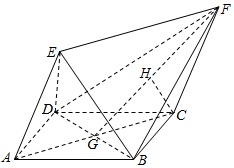
 如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.
如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.分析 (1)由菱形性质得BD⊥AC,由面面垂直的性质得BD⊥面ACFE,由此能证明BD⊥CH.
(2)①由已知得∠GCF=120°,GF=3,由线面垂直得BD⊥GF,从而S△BDF=3,由CH⊥BD,CH⊥GF,得CH⊥平面BDF,由VF-BDC=VC-BDF,利用等积法能求出三棱锥F-BDC的体积.
②求出C到DF的距离,即可求二面角B-DF-C的余弦值.
解答 证明:(1)∵四边形ABCD为菱形,∴BD⊥AC,
又∵面ACFE∩面ABCD=AC,BD?平面ABCD,面ABCD⊥面ACFE,
∴BD⊥面ACFE,
∵CH?面ACFE,∴BD⊥CH;
解:(2)①在△FCG中,$CG=CF=\sqrt{3},CH=\frac{{\sqrt{3}}}{2},CH⊥GF$
∴∠GCF=120°,GF=3.
∵BD⊥面ACFE,GF?面ACFE,
∴BD⊥GF,
${S_{△BDF}}=\frac{1}{2}BD•GF=\frac{1}{2}×2×3=3$.
又∴CH⊥BD,CH⊥GF,
∴BD∩GF=G,BD,GF?平面BDF
∴CH⊥平面BDF
∴${V_{F-BDC}}={V_{C-BDF}}=\frac{1}{3}•{S_{△BDF}}•CH=\frac{1}{3}•3•\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{2}$.
②△CDF中,CD=2,CF=$\sqrt{3}$,DF=$\sqrt{1+9}$=$\sqrt{10}$,
∴cos∠DCF=$\frac{4+3-10}{2×2×\sqrt{3}}$=-$\frac{\sqrt{3}}{4}$,
∴sin∠DCF=$\frac{\sqrt{13}}{4}$,
∴S△DCF=$\frac{1}{2}×2×\sqrt{3}×\frac{\sqrt{13}}{4}$=$\frac{\sqrt{39}}{4}$,
设C到DF的距离为h,则$\frac{1}{2}×\sqrt{10}×h$=$\frac{\sqrt{39}}{4}$,
∴h=$\frac{\sqrt{390}}{20}$,
设二面角B-DF-C的平面角为θ,则tanθ=$\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{390}}{20}}$=$\frac{\sqrt{130}}{13}$,
∴cosθ=$\frac{\sqrt{299}}{23}$.
点评 本题考查异面直线垂直的证明,考查三棱锥的体积的求法,二面角B-DF-C的平面角,考查学生分析解决问题的能力,是中档题,解题时要认真审题,注意线面、面面平行与垂直的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示
2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=2,AD=3,点E是PB的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=2,AD=3,点E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
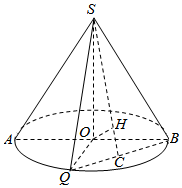 如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知在四棱锥P-ABCD中,底面ABCD为直角梯形,其中CD∥AB,AD⊥AB,侧棱PA⊥底面ABCD,且AD=DC=PA=$\frac{1}{2}$AB=1.
如图所示,已知在四棱锥P-ABCD中,底面ABCD为直角梯形,其中CD∥AB,AD⊥AB,侧棱PA⊥底面ABCD,且AD=DC=PA=$\frac{1}{2}$AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 32 | D. | 128 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com