
 2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示
2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示分析 (1)根据频率分布直方图,利用频率=$\frac{频数}{样本容量}$的关系,即可求出对应的数值;
(2)设A1表示事件“每天遭受DDOS攻击次数的数值高于180”,
A2表示事件“每天遭受DDOS攻击次数的数值低于120”,
B表示事件“在未来3天中,有连续2天的数值高于180,另一天低于120”;
由此求出在未来3天中,有连续2天的数值高于180,另一天低于120的概率值.
解答 解:(1)根据频率分布直方图,得;
数值不超过140的频率为(0.0050+0.0100)×20=0.3,
100×0.3=30,
所以这100天内安全的天数为n=30;
(2)设A1表示事件“每天遭受DDOS攻击次数的数值高于180”,
A2表示事件“每天遭受DDOS攻击次数的数值低于120”,
B表示事件“在未来3天中,有连续2天的数值高于180,另一天低于120”;
所以P(A1)=(0.0075+0.0025)×20=0.2,
P(A2)=0.0050×20=0.1;
所以在未来3天中,有连续2天的数值高于180,另一天低于120的概率:
P(B)=0.2×0.2×0.1+0.1×0.2×0.2=0.008.
点评 本题考查了频率分布直方图的应用问题,也考查了古典概型的概率计算问题,是基础题目.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{{2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | i≥20 | B. | i≤20 | C. | i>21 | D. | i<21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
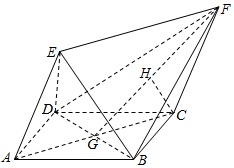 如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.
如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com