
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 利用双曲线的定义、勾股定理、△F1PF2的面积为3,可得c2-a2=3,结合双曲线的离心率e=$\frac{c}{a}$=2,求出a,即可得到双曲线的实轴长2a.
解答 解:设|PF1|=m,|PF2|=n,则|m-n|=2a①
由∠F1PF2=90°,可得m2+n2=4c2,②
则①2-②得:-2mn=4a2-4c2,
即有mn=2c2-2a2,
由△F1PF2的面积为3,
可得$\frac{1}{2}$mn=c2-a2=3,
由双曲线的离心率e=$\frac{c}{a}$=2,
解得c=2,a=1,
故选:C.
点评 本题主要考查双曲线的定义、方程和基本性质.在涉及到与焦点有关的题目时,一般都用定义求解,考查运算能力,属于中档题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 167顷 | B. | 168顷 | C. | 169顷 | D. | 673顷 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示
2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (22015+24031)2016 | B. | 22015+24031 | C. | 2016(22015+24031) | D. | 2016(22016+24032) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过 100km/h人数 | 合计 | |
| 男性驾驶员人数 | 40 | 15 | 55 |
| 女性驾驶员人数 | 20 | 25 | 45 |
| 合计 | 60 | 40 | 100 |
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
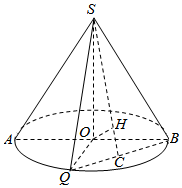 如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com