
| A. | 4 | B. | 6 | C. | 32 | D. | 128 |
分析 利用第八项为1出发,按照规则,逆向逐项即可求出n的所有可能的取值.
解答 解:如果正整数n按照上述规则施行变换后的第八项为1,
则变换中的第7项一定是2,
变换中的第6项一定是4;
变换中的第5项可能是1,也可能是8;
变换中的第4项可能是2,也可是16,
变换中的第4项是2时,变换中的第3项是4,变换中的第2项是1或8,变换中的第1项是2或16
变换中的第4项是16时,变换中的第3项是32或5,变换中的第2项是64或108,变换中的第1项是128,21或20,3
则n的所有可能的取值为2,3,16,20,21,128共6个,
故选:B.
点评 本题主要考查归纳推理的应用,利用变换规则,进行逆向验证是解决本题的关键,考查学生的推理能力.


科目:高中数学 来源: 题型:解答题
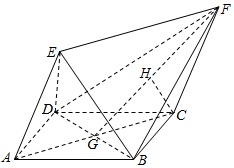 如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.
如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:4 | B. | 1:5 | C. | 1:7 | D. | 1:6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
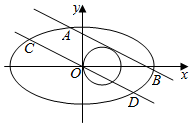 已知椭圆C1:$\frac{x^2}{16}+\frac{y^2}{4}$=1,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{x^2}{16}+\frac{y^2}{4}$=1,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -2 | C. | 2 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com