
分析 首先证明n≥7,取x1=2,x2=x3=x4=x5=-1,则6个形如x1+xi+xj(2≤i<j≤5)的和都等于0,因此n≥7,
再设存在个不同的形如xp+xq+xr(1≤p<q<r≤5)的和都等于0,问题得以解决.
解答 解:首先证明n≥7,取x1=2,x2=x3=x4=x5=-1,则6个形如x1+xi+xj(2≤i<j≤5)的和都等于0,因此n≥7,
设存在个不同的形如xp+xq+xr(1≤p<q<r≤5)的和都等于0,由于$\frac{7×3}{5}>4$,故存在一个xi,它在这7个和式中至少出现5次.
不失一般性,假定i=1.
由于$C_4^2=6$,于是在形如x1+xp+xq(2≤p<q≤5)的和式中,至多一个不为0,
假定在这个和式中,p=2,q=3,于是x1+x2+x4=0,x1+x2+x5=0,x1+x3+x4=0,x1+x3+x5=0,x1+x4+x5=0,
由此易得${x_2}={x_3}={x_4}={x_5}=-\frac{x_1}{2}$.
由于形如(x1,xp,xq)(2≤p<q≤5)的三元组共6个,而7个和式等于0,
所以,一定存在i,j,k≥2满足xi+xj+xk=0,因此xi=xj=xk=0,即所有5个数都是0综上,nmin=7
点评 本题考查了数列以及实数的特征,关键是构造数列成立的条件,属于难题.


科目:高中数学 来源: 题型:解答题
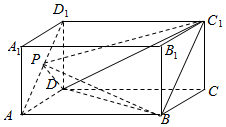 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P为线段AD1上的动点,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P为线段AD1上的动点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点F(0,2)是抛物线x2=2py的焦点.
如图,点F(0,2)是抛物线x2=2py的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:4 | B. | 1:5 | C. | 1:7 | D. | 1:6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,4),(4,-4) | B. | (-4,4),(-4,-4) | C. | (5,$2\sqrt{5}$),(5,$-2\sqrt{5}$) | D. | (-5,$2\sqrt{5}$),(-5,$-2\sqrt{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com