
分析 由a,b,c都是正数,由$\frac{{a}^{2}}{c}$+c≥2$\sqrt{c•\frac{{a}^{2}}{c}}$=2a,求出同样的其它的五个不等式,相加即可得到所求不等式.
解答 证明:a,b,c都是正数,
可得$\frac{{a}^{2}}{c}$+c≥2$\sqrt{c•\frac{{a}^{2}}{c}}$=2a,$\frac{{b}^{2}}{c}$+c≥2$\sqrt{c•\frac{{b}^{2}}{c}}$=2b,
$\frac{{b}^{2}}{a}$+a≥2$\sqrt{a•\frac{{b}^{2}}{a}}$=2b,$\frac{{c}^{2}}{a}$+a≥2$\sqrt{\frac{{c}^{2}}{a}•a}$=2c,
$\frac{{c}^{2}}{b}$+b≥2$\sqrt{b•\frac{{c}^{2}}{b}}$=2c,$\frac{{a}^{2}}{b}$+b≥2$\sqrt{b•\frac{{a}^{2}}{b}}$=2a,
相加,可得$\frac{{a}^{2}+{b}^{2}}{c}$+$\frac{{b}^{2}+{c}^{2}}{a}$+$\frac{{c}^{2}+{a}^{2}}{b}$+2(a+b+c)≥4(a+b+c),
即有a+b+c≤$\frac{{a}^{2}+{b}^{2}}{2c}$+$\frac{{b}^{2}{+c}^{2}}{2a}$+$\frac{{c}^{2}+{a}^{2}}{2b}$,当且仅当a=b=c取得等号.
点评 本题考查不等式的证明,注意运用基本不等式和累加法,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
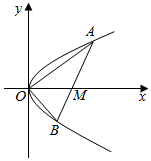 如图,已知直线l与抛物线y2=2px相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M(1,0)线段AB中点坐标(2,1)
如图,已知直线l与抛物线y2=2px相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M(1,0)线段AB中点坐标(2,1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
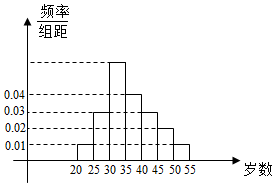 某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.
某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点F(0,2)是抛物线x2=2py的焦点.
如图,点F(0,2)是抛物线x2=2py的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{3}$ | B. | $\frac{25}{8}$ | C. | $\frac{100}{9}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
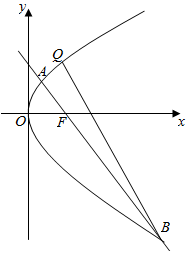 设抛物线y2=2px(p>0)的焦点F,已知抛物线上一点Q,其纵坐标为4,且|QF|=4.
设抛物线y2=2px(p>0)的焦点F,已知抛物线上一点Q,其纵坐标为4,且|QF|=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com