
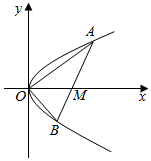
 如图,已知直线l与抛物线y2=2px相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M(1,0)线段AB中点坐标(2,1)
如图,已知直线l与抛物线y2=2px相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M(1,0)线段AB中点坐标(2,1)分析 (1)利用点差法,结合点M(1,0)线段AB中点坐标(2,1),求出p,可得抛物线方程;
(2)直线AB方程x=y+1,代入抛物线方程,利用韦达定理,结合S△AOB=$\frac{1}{2}$|OM||y1-y2|,求△AOB的面积.
解答 解:(1)y12=2px1 ①,y22=2px2②,
两式相减:y12-y22=2px1-2px2得(y1+y2)kAB=2p,代入解得p=1,…(5分)
∴抛物线方程y2=2x; …(6分)
(2)直线AB方程x=y+1,代入抛物线方程y2=2x得y2-2y-2=0①
y1、y2是此方程的两根,y1+y2=2,y1y2=-2,…(8分)
于是S△AOB=$\frac{1}{2}$|OM||y1-y2|=$\frac{1}{2}\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$=$\sqrt{3}$,
∴△AOB的面积为$\sqrt{3}$. …(12分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查点差法的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?=2,φ=$\frac{π}{2}$ | B. | ?=2,φ=π | C. | ?=$\frac{1}{2}$,φ=$\frac{π}{2}$ | D. | ?=$\frac{1}{2}$,φ=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
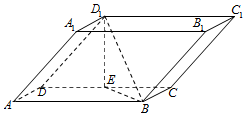 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
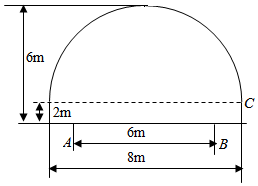 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是3.2米(精确到0.1米)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{2}$ | B. | $\frac{3}{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 36 | C. | $\frac{31}{8}$ | D. | $\frac{63}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com