
分析 依题意,可求得过焦点且倾斜角为135°的直线方程为y=-x+$\frac{a}{4}$,利用抛物线的定义结合题意可求得a,从而可求得抛物线方程.
解答 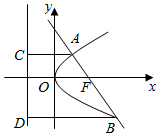 解:依题意,抛物线的焦点坐标为($\frac{a}{4}$,0),则直线方程为y=-x+$\frac{a}{4}$.设直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B分别作准线的垂线,垂足分别为C、D
解:依题意,抛物线的焦点坐标为($\frac{a}{4}$,0),则直线方程为y=-x+$\frac{a}{4}$.设直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B分别作准线的垂线,垂足分别为C、D
则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|=x1+$\frac{a}{4}$+x2+$\frac{a}{4}$
即x1+$\frac{a}{4}$+x2+$\frac{a}{4}$=8.①
又A(x1,y1)、B(x2,y2)是抛物线和直线的交点,
由直线与抛物线消去y,得x2-$\frac{3a}{2}$x+$\frac{{a}^{2}}{16}$=0,
∴x1+x2=$\frac{3a}{2}$.
将其代入①得a=4,
∴所求抛物线方程为y2=4x.
点评 本题考查抛物线的标准方程,突出抛物线定义的应用,考查方程组思想与化归思想的综合运用,考查分析与运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | a<b<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
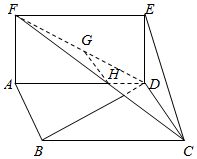 如图,平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面和平面ABCD垂直,G,H分别是DF,FC的中点.
如图,平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面和平面ABCD垂直,G,H分别是DF,FC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
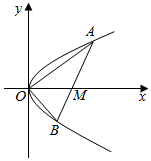 如图,已知直线l与抛物线y2=2px相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M(1,0)线段AB中点坐标(2,1)
如图,已知直线l与抛物线y2=2px相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M(1,0)线段AB中点坐标(2,1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
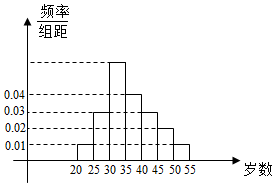 某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.
某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com