
【题目】在极坐标系中,曲线![]() 方程为
方程为![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() ,直线
,直线![]() :
:![]() ,(t为参数,
,(t为参数,![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据公式![]() ,代入即可求得曲线C的直角坐标方程;
,代入即可求得曲线C的直角坐标方程;
(2)将直线的参数方程代入圆的方程,根据参数的几何意义,即可求解.
(1)由ρ2-2![]() ρsin(θ+
ρsin(θ+![]() )-4=0得,
)-4=0得,
ρ2-2ρcosθ-2ρsinθ-4=0.
所以x2+y2-2x-2y-4=0.
曲线C的直角坐标方程为(x-1)2+(y-1)2=6.
(2)将直线l的参数方程代入x2+y2-2x-2y-4=0并整理得,
t2-2(sinα+cosα)t-4=0,
t1+t2=2(sinα+cosα),t1t2=-4<0.
||OA|-|OB||=||t1|-|t2||=|t1+t2|=|2(sinα+cosα)|=|2![]() sin(α+
sin(α+![]() )|
)|
因为0≤α<,所以![]() ≤α+
≤α+![]() <
<![]() ,
,
从而有-2<2![]() sin(α+
sin(α+![]() )≤2
)≤2![]() .
.
所以||OA|-|OB||的取值范围是[0,2![]() ].
].


科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 与
与![]() 的图象在
的图象在![]() 处有相同的切线,求
处有相同的切线,求![]() 的值;
的值;
(2)当![]() 时,若对任意
时,若对任意![]() 和任意
和任意![]() ,总存在不相等的正实数
,总存在不相等的正实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)当![]() 时,设函数
时,设函数![]() 与
与![]() 的图象交于
的图象交于![]()
![]() 两点.求证:
两点.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有15个省三好学生名额分给1、2、3、4共四个班级,其中1班至少2个名额,2班、4班每班至少3个名额,3班最多2个名额,则共有_________种不同分配方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
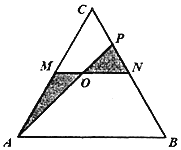
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
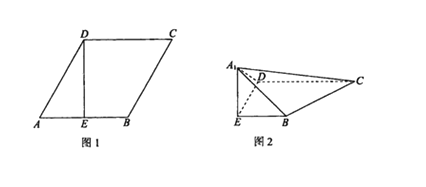
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com