
【题目】如图1,在边长为2的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
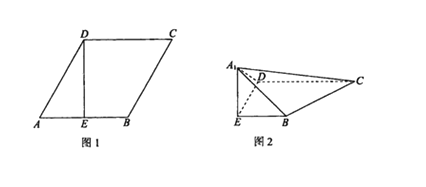
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,且![]()
【解析】
(1)![]() ,
,![]() ,由线面垂直的判定定理得到
,由线面垂直的判定定理得到![]() 平面
平面![]() ,从而有
,从而有![]() ,又
,又![]() ,再由线面垂直的判定定理证明。
,再由线面垂直的判定定理证明。
(2)假设在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ,根据(1)建立空间直角坐标系,设
,根据(1)建立空间直角坐标系,设![]() ,则
,则![]() ,所以
,所以![]() ,若使平面
,若使平面![]() 平面
平面![]() ,分别求得两个平面的法向量,再通过两个法向量数量积为零求解.
,分别求得两个平面的法向量,再通过两个法向量数量积为零求解.
(1)证明:因为![]() 于点
于点![]() ,
,
所以![]() ,
,
![]() ,
,![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,
![]()
![]() ,
,
![]() 平面
平面![]() .
.
(2)假设在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() .
.
根据(1)建立如图所示空间直角坐标系:

则![]() ,
,![]() ,
,
设![]() ,
,
则![]() ,所以
,所以![]() ,
,
所以![]() ,
,
设平面![]() 一个法向量为:
一个法向量为:![]() ,
,
则 ,即
,即 ,
,
令![]() ,所以
,所以![]() ,
,
设平面![]() 一个法向量为:
一个法向量为:![]() ,
,
则 ,即
,即 ,
,
令![]() ,所以
,所以![]() ,
,
因为平面![]() 平面
平面![]() ,
,
所以![]() ,即
,即![]()
解得![]() .
.
所以在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ,且
,且![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 方程为
方程为![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() ,直线
,直线![]() :
:![]() ,(t为参数,
,(t为参数,![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的四棱锥![]() 中,
中, ![]() 为底面正方形的中心,
为底面正方形的中心, ![]() ,
,![]() 分别为侧棱
分别为侧棱![]() ,
,![]() 的中点,有下列结论正确的有:( )
的中点,有下列结论正确的有:( )

A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和点
和点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,
,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于另一点
交于另一点![]() .给出以下判断:
.给出以下判断:
①直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() ;
;
②![]() 轴;
轴;
③以![]() 为直径的圆与抛物线准线相切.
为直径的圆与抛物线准线相切.
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高三年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
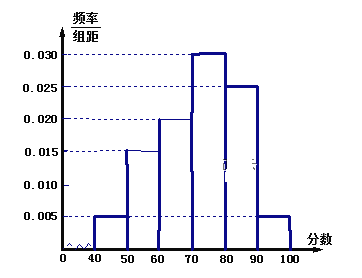
(1)估计这次考试的及格率(60分及以上为及格)和平均分;
(2)按分层抽样从成绩是80分以上(包括80分)的学生中选取6人,再从这6人中选取两人作为代表参加交流活动,求他们在不同分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为( )
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为( )
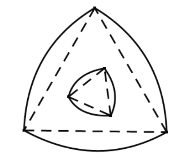
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com