
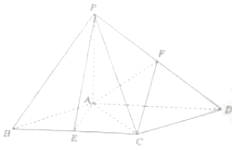
 已知四棱锥P-ABCD的底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,点E、F分别为BC、PD的中点,PA=AB=2.
已知四棱锥P-ABCD的底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,点E、F分别为BC、PD的中点,PA=AB=2.分析 (Ⅰ)由PA⊥底面ABCD,得PA⊥AE.再由已知得△ABC为等边三角形,可得AE⊥BC,即AE⊥AD.然后由线面垂直的判定可得AE⊥平面PAD;
(Ⅱ)令多面体PAECF的体积为V,则V=VP-AEC+VC-PAF.然后结合已知分别求出两个三棱锥的体积得答案.
解答 (Ⅰ)证明:由PA⊥底面ABCD,得PA⊥AE.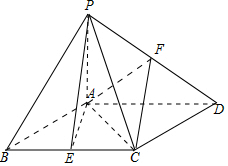
底面ABCD为菱形,∠ABC=60°,得△ABC为等边三角形,
又∵E为BC的中点,得AE⊥BC,∴AE⊥AD.
∵PA∩AD=A,∴AE⊥平面PAD;
(Ⅱ)解:令多面体PAECF的体积为V,则V=VP-AEC+VC-PAF.
∵底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,
点E、F分别为BC、PD的中点,PA=AB=2,
∴${V_{P-AEC}}=\frac{1}{3}×(\frac{1}{2}×AE×EC)×PA$=$\frac{1}{3}×(\frac{1}{2}×\sqrt{3}×1)×2=\frac{{\sqrt{3}}}{3}$;
${V_{C-PAF}}=\frac{1}{3}×(\frac{1}{2}×PA×PF×sin∠APF)$×$AE=\frac{1}{3}×(\frac{1}{2}×2×\sqrt{2}×sin45°)$×$\sqrt{3}=\frac{{\sqrt{3}}}{3}$.
∴多面体PAECF的体积为$V=\frac{{\sqrt{3}}}{3}+\frac{{\sqrt{3}}}{3}=\frac{{2\sqrt{3}}}{3}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1,2} | B. | {-1,2} | C. | {1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com