
分析 由已知求出$\overrightarrow{a}•\overrightarrow{b}$的值,再由(m$\overrightarrow{a}+\overrightarrow{b}$)⊥$\overrightarrow{a}$,得(m$\overrightarrow{a}+\overrightarrow{b}$)•$\overrightarrow{a}$=0,展开后得答案.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=4,
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°=2×4×(-\frac{1}{2})=-4$,
又(m$\overrightarrow{a}+\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴(m$\overrightarrow{a}+\overrightarrow{b}$)•$\overrightarrow{a}$=$m|\overrightarrow{a}{|}^{2}+\overrightarrow{a}•\overrightarrow{b}=4m-4=0$,解得m=1.
故答案为:1.
点评 本题考查平面向量的数量积运算,考查向量垂直与数量积间的关系,是中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
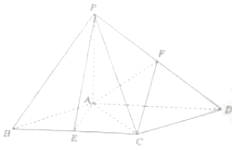 已知四棱锥P-ABCD的底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,点E、F分别为BC、PD的中点,PA=AB=2.
已知四棱锥P-ABCD的底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,点E、F分别为BC、PD的中点,PA=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
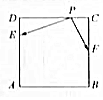 如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).
如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com