解:(Ⅰ)由
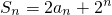
①,得
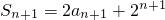
②,
②-①得,a
n+1=2a
n+1-2a
n+2
n,即
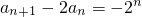
,
则
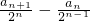
=
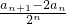
=
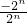
=-1,为常数,
所以数列
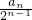
是等差数列,且公差为-1,
由S
1=2a
1+2解得a
1=-2,
所以
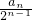
=-2+(n-1)•(-1)=-n-1,
所以
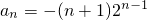
;
(Ⅱ)由(Ⅰ)得,
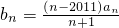
=
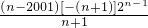
=(2011-n)•2
n-1,
则
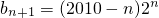
,当n=2011时,b
n=0,
当n>2011时,b
n<0,令
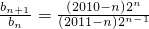
=
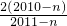
≥1,得n>2011,所以b
n>b
n+1,即b
2012>b
2013>…,
当n≤2010时,b
n>0,令
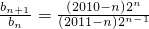
=
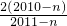
≥1,解得n≤2009,
所以n≤2009时,b
n+1≥b
n,所以0<b
1<b
2<b
3<…<b
2009=b
2010,
综上,b
1<b
2<b
3<…b
2012>b
2013>…,
所以数列{b
n}存在最大值项,为第2009项或2010项;
(Ⅲ)由(Ⅰ)知,
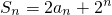
=2[-(n+1)•2
n-1]+2
n=-n•2
n,
所以|S
n|=n•2
n,
则T
n=|S
1|+|S
2|+|S
3|+…+|S
n|=1•2
1+2•2
2+3•2
3+…+n•2
n①,
2T
n=2
2+2•2
3+3•2
4+…+n•2
n+1②,
①-②得,-T
n=2+2
2+2
3+…+2
n-n•2
n+1=
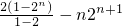
=(1-n)•2
n+1-2,
所以T
n=(n-1)•2
n+1+2,
所以
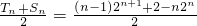
=
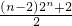
=(n-2)•2
n-1+1,
又
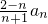
=
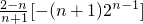
=(n-2)•2
n-1,
所以
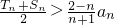
.
分析:(Ⅰ)由
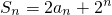
,得
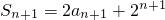
,两式相减可得数列递推式,借助该递推式可计算
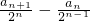
为常数,由等差数列定义即可证明为等差数列,从而可求得
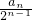
,进而求得a
n;
(Ⅱ)由(Ⅰ)可求出b
n,据其通项可判断数列{b
n}各项符号,通过作商可判断数列的单调性,由单调性即可判断其最大值项;
(Ⅲ)由(Ⅰ)可求得S
n,从而得|S
n|,由错位相减法可求出T
n,进而得到
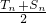
,由(Ⅰ)易求
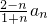
,两者大小关系容易判断;
点评:本题考查等差数列、数列求和,考查错位相减法对数列求和,考查学生的运算能力、分析解决问题的能力,综合性较强.

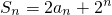 ,
,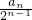 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;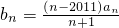 ,求数列{bn}是否存在最大值项,若存在,说明是第几项,若不存在,请说明理由;
,求数列{bn}是否存在最大值项,若存在,说明是第几项,若不存在,请说明理由;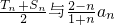 的大小.
的大小.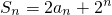 ①,得
①,得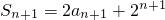 ②,
②,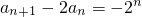 ,
,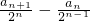 =
=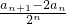 =
=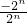 =-1,为常数,
=-1,为常数,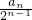 是等差数列,且公差为-1,
是等差数列,且公差为-1,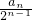 =-2+(n-1)•(-1)=-n-1,
=-2+(n-1)•(-1)=-n-1,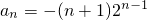 ;
;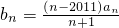 =
=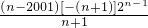 =(2011-n)•2n-1,
=(2011-n)•2n-1,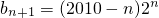 ,当n=2011时,bn=0,
,当n=2011时,bn=0,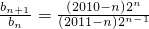 =
=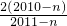 ≥1,得n>2011,所以bn>bn+1,即b2012>b2013>…,
≥1,得n>2011,所以bn>bn+1,即b2012>b2013>…,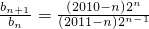 =
=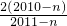 ≥1,解得n≤2009,
≥1,解得n≤2009,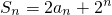 =2[-(n+1)•2n-1]+2n=-n•2n,
=2[-(n+1)•2n-1]+2n=-n•2n,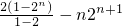 =(1-n)•2n+1-2,
=(1-n)•2n+1-2,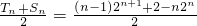 =
=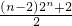 =(n-2)•2n-1+1,
=(n-2)•2n-1+1,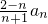 =
=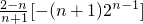 =(n-2)•2n-1,
=(n-2)•2n-1,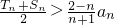 .
.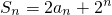 ,得
,得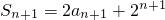 ,两式相减可得数列递推式,借助该递推式可计算
,两式相减可得数列递推式,借助该递推式可计算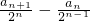 为常数,由等差数列定义即可证明为等差数列,从而可求得
为常数,由等差数列定义即可证明为等差数列,从而可求得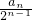 ,进而求得an;
,进而求得an;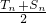 ,由(Ⅰ)易求
,由(Ⅰ)易求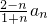 ,两者大小关系容易判断;
,两者大小关系容易判断;

 名校课堂系列答案
名校课堂系列答案