
【题目】已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设 ![]() ,则x+y的取值范围 .
,则x+y的取值范围 . 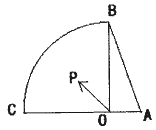
【答案】[﹣2,1]
【解析】解:以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,如图所示;

则A(1,0),B(0,2),
∴ ![]() =x
=x ![]() +y
+y ![]() =(x,0)+(0,2y)=(x,2y),
=(x,0)+(0,2y)=(x,2y),
则x,y满足条件 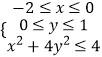 ,
,
作出可行域如图所示, 
令z=x+y,化目标函数为y=﹣x+z,
由图可知,当直线y=﹣x+z过点(0,1)时,直线在y轴上的截距最大,z有最大值1;
当直线y=﹣x+z过点(﹣2,0)时,直线在y轴上的截距最小,z有最小值﹣2;
则x+y的取值范围是[﹣2,1].
故答案为:[﹣2,1].
以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,
表示出点A、B的坐标,得出 ![]() 的坐标表示,从而求出x,y满足的约束条件,
的坐标表示,从而求出x,y满足的约束条件,
再利用线性规划的方法求出目标函数z=x+y的最值即可得出结果.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
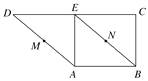
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2 , |AB|=4,|F1F2|=2 ![]() ,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
(Ⅰ)求椭圆E的离心率;
(Ⅱ)若m>0,设直线AD、BC的斜率分别为k1、k2 , 求 ![]() 的取值范围.
的取值范围.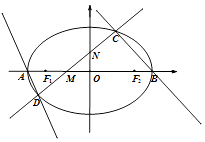
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为 ![]() .
.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明 ![]() 为定值,并求△AOB的面积的最大值.
为定值,并求△AOB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(-x-1)=f(x-1),其图象过点(0,1),且与x轴有唯一交点。
(1)求f(x)的解析式;
(2)设函数g(x)=f(x)-(2+a)x,求g(x)在[1,2]上的最小值h(a)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com