
【题目】已知椭圆![]() (
(![]() )经过
)经过![]() 与
与 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,椭圆
两点,椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:
(1)由题意将点的坐标代入椭圆方程即可求得椭圆的方程为![]() ;
;
(2)利用(1)中求得的椭圆方程结合题意分类讨论可证得![]() 为定值2.
为定值2.
试题解析:
(1)将![]() 与(
与(![]() ,
,![]() )两点代入椭圆C的方程,
)两点代入椭圆C的方程,
得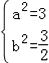 解得
解得![]() . ∴椭圆PM2的方程为
. ∴椭圆PM2的方程为![]() .
.
(2)由|MA|=|MB|,知M在线段AB的垂直平分线上,由椭圆的对称性知A、B关于原点对称.
①若点A、B是椭圆的短轴顶点,则点M是椭圆的一个长轴顶点,此时
![]() =
=![]() .
.
同理,若点A、B是椭圆的长轴顶点,则点M在椭圆的一个短轴顶点,此时
![]() =
=![]() .
.
②若点A、B、M不是椭圆的顶点,设直线l的方程为y=kx(k≠0),
则直线OM的方程为![]() ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),
由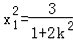 解得
解得![]() ,
,![]() ,
,
∴![]() =
=![]() ,同理
,同理![]() ,
,
所以![]() =2×
=2×![]() +
+![]() =2,
=2,
故![]() =2为定值.
=2为定值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中:
①线性回归直线方程![]() 恒过样本中心
恒过样本中心![]() ;
;
②用相关指数![]() 可以刻画回归的效果,值越小说明模型的拟合效果越好;
可以刻画回归的效果,值越小说明模型的拟合效果越好;
③随机误差是引起预报值![]() 和真实值
和真实值![]() 之间存在误差的原因之一,其大小取决于随机误差的方差;
之间存在误差的原因之一,其大小取决于随机误差的方差;
④在含有一个解释变量的线性模型中,相关指数![]() 等于相关系数
等于相关系数![]() 的平方.
的平方.
其中真命题为 _________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,正三角形PAC所在平面与等腰三角形ABC所在平面互相垂直,AB=BC,O是AC中点,OH⊥PC于H.
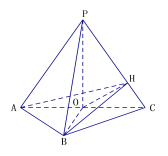
(1)证明:PC⊥平面BOH;
(2)若![]() ,求二面角A-BH-O的余弦值.
,求二面角A-BH-O的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )
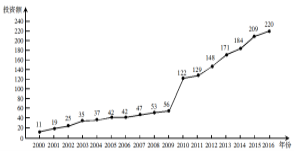
A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com