
【题目】已知函数![]()
(I)讨论![]() 的单调性;
的单调性;
(II)当![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,都有
,都有![]() ?若存在求出
?若存在求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(I)当![]() ,
,![]() 在
在![]() 为增函数;当
为增函数;当![]() ,
,![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数; (II)
为减函数; (II)![]() .
.
【解析】
(I)先求得函数![]() 的定义域,对其求导后对
的定义域,对其求导后对![]() 分成
分成![]() 两类,讨论函数的单调区间.(II)将不等式
两类,讨论函数的单调区间.(II)将不等式![]() 等价转化为
等价转化为![]() 恒成立,构造函数
恒成立,构造函数![]() ,利用其导数恒为非负数列不等式,分离常数后利用基本不等式求得
,利用其导数恒为非负数列不等式,分离常数后利用基本不等式求得![]() 的取值范围.
的取值范围.
(I)![]() 的定义域为
的定义域为![]()
![]() ,
,
当![]() ,则
,则![]() ,
,![]() 在
在![]() 为增函数,
为增函数,
![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以,当![]()
![]() span>,
span>,![]() ,
,![]() 在
在![]() 为增函数;
为增函数;
当![]()
![]() ,
,![]() ,
,![]() 在
在![]() 为减函数,
为减函数,
综上所述,当![]() ,
,![]() 在
在![]() 为增函数;
为增函数;
当![]() ,
,![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数。
为减函数。
(II)不妨设![]() ,则
,则![]() ,
,
假设存在实数![]() ,使得
,使得![]()
![]() ,都有
,都有![]() ,
,
则![]() 恒成立,
恒成立,
即![]() 恒成立,(*)
恒成立,(*)
设![]() ,即(*)等价于
,即(*)等价于![]() 在
在![]() 为单调递增
为单调递增
等价于![]() 在
在![]() 恒成立,
恒成立,
等价于![]() 在
在![]() 恒成立,
恒成立,
等价于![]() 在
在![]() 恒成立,
恒成立,
∴![]() ,当且仅当
,当且仅当![]() 取等号,
取等号,
∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() ,圆
,圆![]() 的方程为
的方程为![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 能否作一条直线
能否作一条直线![]() ,与点
,与点![]() 的轨迹交于
的轨迹交于![]() 两点,且点
两点,且点![]() 为线段
为线段![]() 的中点?若存在,求出直线
的中点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于空间向量的命题中,正确的有______.
①若向量![]() ,
,![]() 与空间任意向量都不能构成基底,则
与空间任意向量都不能构成基底,则![]() ;
;
②若非零向量![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,则有
,则有![]() ;
;
③若![]() ,
,![]() ,
,![]() 是空间的一组基底,且
是空间的一组基底,且![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
④若向量![]() ,
,![]() ,
,![]() ,是空间一组基底,则
,是空间一组基底,则![]() ,
,![]() ,
,![]() 也是空间的一组基底.
也是空间的一组基底.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,点
,点![]() 在平面
在平面![]() 的射影为
的射影为![]() ,
,![]() 为棱
为棱![]() 上一点,
上一点,
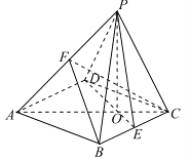
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E,Q分别是BC和PC的中点.
,E,Q分别是BC和PC的中点.
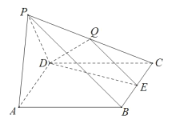
(I)求直线BQ与平面PAB所成角的正弦值;
(Ⅱ)求二面角E-DQ-P的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com