
【题目】过点![]() 作抛物线
作抛物线![]() 的两条切线, 切点分别为
的两条切线, 切点分别为![]() ,
, ![]() .
.
(1) 证明: ![]() 为定值;
为定值;
(2) 记△![]() 的外接圆的圆心为点
的外接圆的圆心为点![]() , 点
, 点![]() 是抛物线
是抛物线![]() 的焦点, 对任意实数
的焦点, 对任意实数![]() , 试判断以
, 试判断以![]() 为直径的圆是否恒过点
为直径的圆是否恒过点![]() ? 并说明理由.
? 并说明理由.
【答案】(I)详见解析;(II)详见解析.
【解析】试题分析:(Ⅰ)对![]() 求导,得到直线
求导,得到直线![]() 的斜率为
的斜率为![]() ,进一步得到直线
,进一步得到直线![]() 的方程为
的方程为![]() . 将点点
. 将点点![]() 代入直线
代入直线![]() 方程,整理得
方程,整理得![]() .
.
同理, ![]() . 又
. 又![]() , 所以
, 所以![]() 为定值.
为定值.
(Ⅱ)由题意可得)直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ①
. ①
同理直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ②
. ②
由①②解得点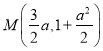 . 又 抛物线
. 又 抛物线![]() 的焦点为
的焦点为![]() 则
则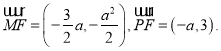 由
由![]() , 可得
, 可得![]() 所以以
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
试题解析:
(Ⅰ) 法1:由![]() ,得
,得![]() ,所以
,所以![]() . 所以直线
. 所以直线![]() 的斜率为
的斜率为![]() .
.
因为点![]() 和
和![]() 在抛物线
在抛物线![]() 上, 所以
上, 所以![]() ,
,![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
因为点![]() 在直线
在直线![]() 上,
上,
所以![]() ,即
,即![]() .
.
同理, ![]() .
.
所以![]() 是方程
是方程![]() 的两个根.
的两个根.
所以![]() .
.
又![]() ,
,
所以![]() 为定值.
为定值.
法2:设过点![]() 且与抛物线
且与抛物线![]() 相切的切线方程为
相切的切线方程为![]() ,
,
由![]() 消去
消去![]() 得
得![]() ,
,
由![]() , 化简得
, 化简得![]() .
.
所以![]() .
.
由![]() ,得
,得![]() ,所以
,所以![]() .
.
所以直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
所以![]() , 即
, 即![]() .
.
又![]() ,
,
所以![]() 为定值.
为定值.
(Ⅱ) 法1:直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
由于![]() ,
,![]() ,
,
所以直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ①
. ①
同理直线![]() 的垂直平分线方程为
的垂直平分线方程为![]() . ②
. ②
由①②解得![]() ,
, ![]() ,
,
所以点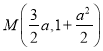 .
.
抛物线![]() 的焦点为
的焦点为![]() 则
则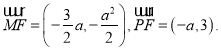
由于![]() ,
,
所以![]()
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
另法: 以![]() 为直径的圆的方程为
为直径的圆的方程为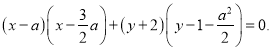
把点![]() 代入上方程,知点
代入上方程,知点![]() 的坐标是方程的解.
的坐标是方程的解.
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
法2:设点![]() 的坐标为
的坐标为![]() ,
,
则△![]() 的外接圆方程为
的外接圆方程为![]() ,
,
由于点![]() 在该圆上,
在该圆上,
则![]() ,
,
![]() .
.
两式相减得![]() , ①
, ①
由(Ⅰ)知![]() ,代入上式得
,代入上式得
![]() ,
,
当![]() 时, 得
时, 得![]() , ②
, ②
假设以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则
,则![]() 即
即![]() ,
,
得![]() , ③
, ③
由②③解得![]() ,
,
所以点![]() .
.
当![]() 时, 则
时, 则![]() ,点
,点![]() .
.
所以以![]() 为直径的圆恒过点
为直径的圆恒过点![]()


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() ;④当
;④当![]() 秒时,
秒时, ![]() ∽
∽![]() ;⑤当
;⑤当![]() 的面积为
的面积为![]() 时,时间
时,时间![]() 的值是
的值是![]() 或
或![]() ;其中正确的结论是( )
;其中正确的结论是( )
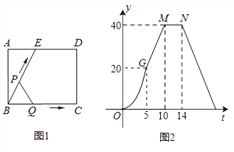
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名;乙协会的运动员
名;乙协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名.从这
名.从这![]() 名运动员中随机选择
名运动员中随机选择![]() 人参加比赛.
人参加比赛.
(1)设![]() 为事件“选出的
为事件“选出的![]() 人中恰有
人中恰有![]() 名种子选手,且这
名种子选手,且这![]() 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的
为选出的![]() 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知底角为![]() 的等腰梯形
的等腰梯形![]() ,底边
,底边![]() 长为12,腰长为
长为12,腰长为![]() ,当一条垂直于底边
,当一条垂直于底边![]() (垂足为
(垂足为![]() )的直线
)的直线![]() 从左至右移动(与梯形
从左至右移动(与梯形![]() 有公共点)时,直线
有公共点)时,直线![]() 把梯形分成两部分.
把梯形分成两部分.
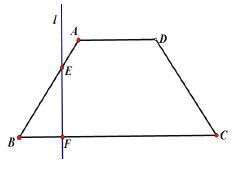
(1)令![]() ,试写出直线右边部分的面积
,试写出直线右边部分的面积![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)在(1)的条件下,令![]() .构造函数
.构造函数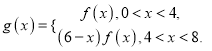
①判断函数![]() 在
在![]() 上的单调性;
上的单调性;
②判断函数![]() 在定义域内是否具有单调性,并说明理由.
在定义域内是否具有单调性,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
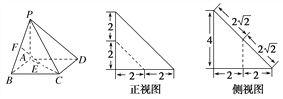
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中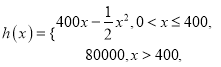
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
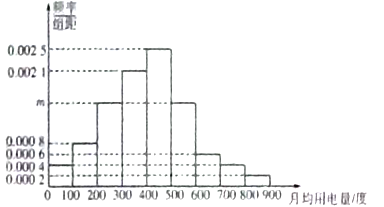
(Ⅰ)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的![]() ,得曲线C.
,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l: ![]() 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com