
已知函数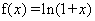 ,
,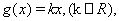
(1)证明:当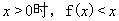 ;
;
(2)证明:当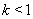 时,存在
时,存在 ,使得对
,使得对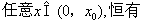
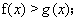
(3)确定k的所以可能取值,使得存在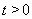 ,对任意的
,对任意的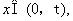 恒有
恒有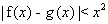 .
.
解法一:(1)令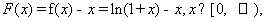 则有
则有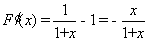
当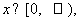
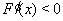 ,所以
,所以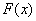 在
在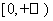 上单调递减,
上单调递减,
故当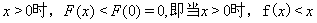 .
.
(2)令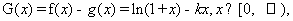 则有
则有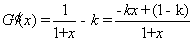
当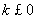
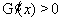 ,所以
,所以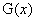 在
在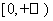 上单调递增,
上单调递增, 
故对任意正实数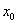 均满足题意.
均满足题意.
当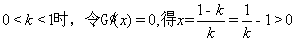 .
.
取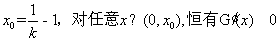 ,所以
,所以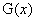 在
在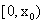 上单调递增,
上单调递增,  ,即
,即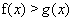 .
.
综上,当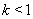 时,总存在
时,总存在 ,使得对任意的
,使得对任意的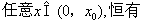
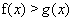 .
.
(3)当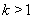 时,由(1)知,对于
时,由(1)知,对于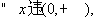
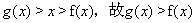 ,
,
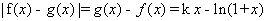 ,
,
令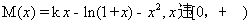 ,则有
,则有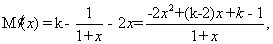
故当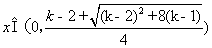 时,
时,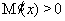 ,
,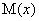 在
在 上单调递增,故
上单调递增,故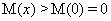 ,即
,即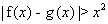 ,所以满足题意的t不存在.
,所以满足题意的t不存在.
当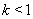 时,由(2)知存在
时,由(2)知存在 ,使得对任意的
,使得对任意的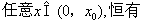
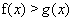 .
.
此时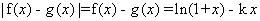 ,
,
令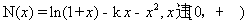 ,则有
,则有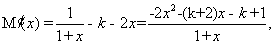
故当 时,
时, ,
,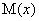 在
在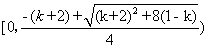 上单调递增,故
上单调递增,故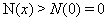 ,即
,即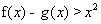 ,记
,记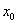 与
与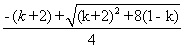 中较小的为
中较小的为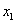 ,
,
则当 ,故满足题意的t不存在.
,故满足题意的t不存在.
当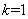 ,由(1)知,
,由(1)知,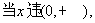
 ,
,
令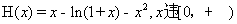 ,则有
,则有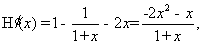
当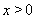 时,
时,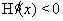 ,所以
,所以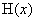 在
在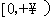 上单调递减,故
上单调递减,故 ,
,
故当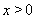 时,恒有
时,恒有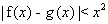 ,此时,任意实数t满足题意.
,此时,任意实数t满足题意.
综上,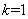 .
.
解法二:(1)(2)同解法一.
(3)当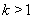 时,由(1)知,对于
时,由(1)知,对于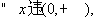
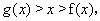 ,
,
故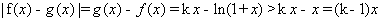 ,
,
令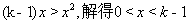 ,
,
从而得到当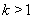 时,
时,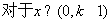 恒有
恒有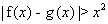 ,所以满足题意的t不存在.
,所以满足题意的t不存在.
当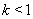 时,取
时,取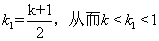
由(2)知存在 ,使得
,使得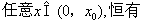
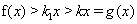 .
.
此时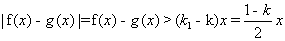 ,
,
令 ,此时
,此时 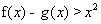 ,
,
记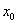 与
与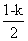 中较小的为
中较小的为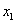 ,则当
,则当 ,
,
故满足题意的t不存在.
当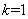 ,由(1)知,
,由(1)知,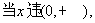
 ,
,
令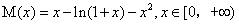 ,则有
,则有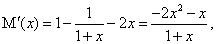
当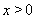 时,
时,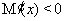 ,所以
,所以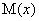 在
在 上单调递减,故
上单调递减,故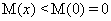 ,
,
故当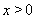 时,恒有
时,恒有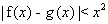 ,此时,任意实数t满足题意.
,此时,任意实数t满足题意.
综上,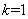 .
.


科目:高中数学 来源: 题型:
设直线l与抛物线y2=4x相较于A,B两点,与圆C:(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB中点,若这样的直线l恰有4条,则r的取值范围是
(A)(1,3) (B)(1,4) (C)(2,3) (D)(2,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
一个二元码是由0和1组成的数字串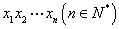 ,其中
,其中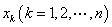 称为第
称为第 位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)
位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)
已知某种二元码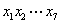 的码元满足如下校验方程组:
的码元满足如下校验方程组: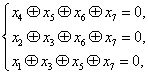
其中运算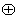 定义为:
定义为: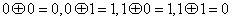 .
.
现已知一个这种二元码在通信过程中仅在第 位发生码元错误后变成了1101101,那么利用上述校验方程组可判定
位发生码元错误后变成了1101101,那么利用上述校验方程组可判定 等于 .
等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为
A.36π B.64π C.144π D.256π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com