
我国是水资源相对匮乏的国家,为鼓励节约用水,某市打算制定一项水费措施,规定每季度每人用水不超过5吨时,每吨水费的价格(基本消费价)为1.3元,若超过5吨而不超过6吨时,超过部分的水费加收200%,若超过6吨而不超过7吨时,超过部分的水费加收400%,如果某人本季度实际用水量为x(x≤7)吨,试计算本季度他应缴纳的水费.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
命题“∀x>0,x2+x>0”的否定是( ).
A.∃x0>0,x20+x0>0 B.∃x0>0,x20+x0≤0
C.∀x>0,x2+x≤0 D.∀x≤0,x2+x>0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=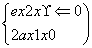 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题:
①函数f(x)的最小值是-1;
②函数f(x)在R上是单调函数;
③若f(x)>0在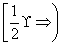 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1;
④对任意的x1<0,x2<0且x1≠x2,恒有f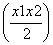 <
<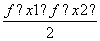 .
.
其中正确命题的序号是__________(写出所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com