
| A. | 2z | B. | -2z | C. | 2$\overline{z}$ | D. | -2$\overline{z}$ |
分析 根据题意和复数代数形式的混合运算求出z2、z3,代入z+z2-z3化简即可.
解答 解:∵z=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,∴${z}^{2}=(\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{2}$=$-\frac{1}{2}+\frac{\sqrt{3}}{2}i$,
∴${z}^{3}={(\frac{1}{2}+\frac{\sqrt{3}}{2}i)}^{3}$=$(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)(\frac{1}{2}+\frac{\sqrt{3}}{2}i)$=-1,
即z+z2-z3=$\frac{1}{2}+\frac{\sqrt{3}}{2}i+(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)-(-1)$=1$+\sqrt{3}i$=2z,
故选A.
点评 本题考查了复数代数形式的混合运算的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第16项 | B. | 第24项 | C. | 第26项 | D. | 第28项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{364}$ | B. | $\frac{1}{121}$ | C. | $\frac{120}{121}$ | D. | $\frac{363}{364}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
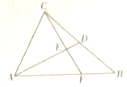 如图△ABC,点D是BC中点,$\overrightarrow{AF}$=2$\overrightarrow{FB}$,CF和AD交于点E,设$\overrightarrow{AD}$=a,$\overrightarrow{AB}$=b.
如图△ABC,点D是BC中点,$\overrightarrow{AF}$=2$\overrightarrow{FB}$,CF和AD交于点E,设$\overrightarrow{AD}$=a,$\overrightarrow{AB}$=b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com