
已知椭圆 :
: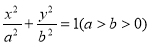 的短轴长为
的短轴长为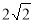 ,且斜率为
,且斜率为 的直线
的直线 过椭圆
过椭圆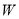 的焦点及点
的焦点及点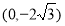 .
.
(1)求椭圆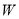 的方程;
的方程;
(2)已知直线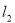 过椭圆
过椭圆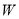 的左焦点
的左焦点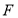 ,交椭圆于点P、Q.
,交椭圆于点P、Q.
(ⅰ)若满足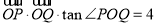 (
(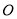 为坐标原点),求
为坐标原点),求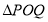 的面积;
的面积;
(ⅱ)若直线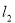 与两坐标轴都不垂直,点
与两坐标轴都不垂直,点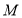 在
在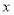 轴上,且使
轴上,且使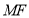 为
为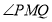 的一条角平分线,则称点
的一条角平分线,则称点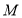 为椭圆
为椭圆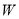 的“特征点”,求椭圆
的“特征点”,求椭圆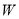 的特征点.
的特征点.
(1)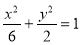 ;(2)(ⅰ)2,(ⅱ)
;(2)(ⅰ)2,(ⅱ)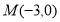
【解析】
试题分析:(1)由短轴长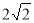 得
得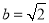 ,由焦点和点
,由焦点和点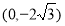 可算出斜率为
可算出斜率为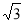 ,可以得到焦点坐标,所以可以得椭圆的方程。(2)(ⅰ)由向量的数量积公式及三角形面积公式可得出结果。(ⅱ)设直线
,可以得到焦点坐标,所以可以得椭圆的方程。(2)(ⅰ)由向量的数量积公式及三角形面积公式可得出结果。(ⅱ)设直线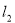 的方程,但是不需要求
的方程,但是不需要求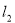 的方程,通过与椭圆联立方程组进行求解。
的方程,通过与椭圆联立方程组进行求解。
试题解析:(1)由题意可知,直线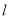 的方程为
的方程为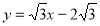 , 1分
, 1分
∵直线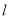 过椭圆
过椭圆 的焦点,∴该焦点坐标为
的焦点,∴该焦点坐标为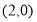 ∴
∴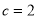 2分
2分
又椭圆 的短轴长为
的短轴长为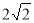 ,∴
,∴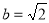 ,∴
,∴ 3分
3分
∴椭圆 的方程为
的方程为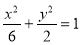 4分
4分
(2)(ⅰ)∵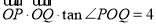
∴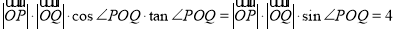 6分
6分
∴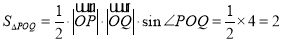 8分
8分
(ⅱ)设特征点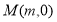 ,左焦点为
,左焦点为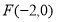 ,可设直线PQ的方程为
,可设直线PQ的方程为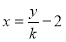 ,
,
由 消去
消去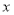 得
得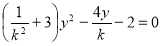
设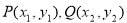 ,则
,则
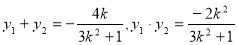 10分
10分
∵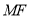 为
为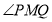 的一条角平分线,
的一条角平分线,
∴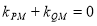 ,即
,即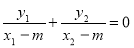 12分
12分
又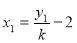 ,
,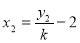 ,代入上式可得
,代入上式可得
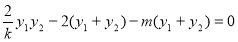
∴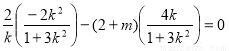 ,解得
,解得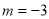
∴椭圆C的特征点为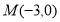 . 14分
. 14分
考点:圆锥曲线与其他知识的综合


科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
A.12, 24, 15, 9 B.9, 12, 12, 7 C.8, 15, 12, 5 D.8, 16, 10, 6
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:选择题
在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,能被5整除的个数有( )
A.512 B.192 C.240 D.108
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考理科数学试卷(解析版) 题型:选择题
用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( )
A.假设至少有一个钝角 B.假设至少有两个钝角
C.假设没有一个钝角 D.假设没有一个钝角或至少有两个钝角
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考文科数学试卷(解析版) 题型:解答题
已知复数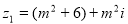 ,
,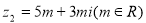 .
.
(1)若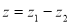 为纯虚数,求实数
为纯虚数,求实数 的值;
的值;
(2)当 =1时,若
=1时,若 ,请问复数
,请问复数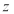 在复平面内对应的点在第几象限?
在复平面内对应的点在第几象限?
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考文科数学试卷(解析版) 题型:选择题
把正整数按右图所示的规律排序,则从2013到2015的箭头方向依次为( )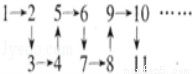
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知函数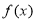 是定义在
是定义在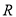 上的奇函数,当
上的奇函数,当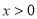 时,
时,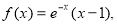 给出以下命题:
给出以下命题:
①当
 时,
时,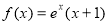 ; ②函数
; ②函数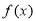 有五个零点;
有五个零点;
③对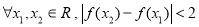 恒成立.
恒成立.
④若关于 的方程
的方程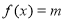 有解,则实数
有解,则实数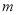 的取值范围是
的取值范围是 ;
;
其中,正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
极坐标系的极点是直角坐标系的原点,极轴为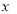 轴正半轴.已知曲线
轴正半轴.已知曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (其中
(其中 为参数)
为参数)
(1)求曲线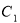 的直角坐标方程和曲线
的直角坐标方程和曲线 的普通方程;
的普通方程;
(2)判断曲线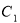 和曲线
和曲线 的位置关系;若曲线
的位置关系;若曲线 和曲线
和曲线 相交,求出弦长.
相交,求出弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com