
分析 由两直线平行得到x的系数之比等于y的系数之比不等于常数项之比求出a的值,然后把第二个方程等号两边都除以2后,利用两平行线间的距离公式表示出关于c的方程,求出方程的解即可得到c的值,把a和c的值代入即可求出所求式子的值.
解答 解:由题意得,$\frac{3}{6}$=$\frac{-2}{a}$≠$\frac{-1}{c}$,∴a=-4,c≠-2,
则6x+ay+c=0可化为3x-2y+$\frac{c}{2}$=0,
由两平行线间的距离公式,得$\frac{|\frac{c}{2}+1|}{\sqrt{13}}$=$\frac{2\sqrt{13}}{13}$,即|$\frac{c}{2}$+1|=2
解得c=2或-6,
故答案为:2或-6.
点评 此题考查学生掌握两直线平行的条件,灵活运用两平行线间的距离公式化简求值,是一道基础题.


科目:高中数学 来源: 题型:解答题
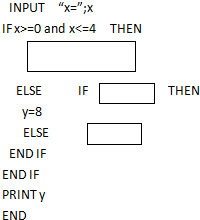 函数y=$\left\{\begin{array}{l}2x,0≤x≤4\\ 8,4<x≤8\\ 2(12-x),8<x≤12\end{array}$,填补方框内的内容完成函数的函数值的程序.
函数y=$\left\{\begin{array}{l}2x,0≤x≤4\\ 8,4<x≤8\\ 2(12-x),8<x≤12\end{array}$,填补方框内的内容完成函数的函数值的程序.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{27}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月 份 | 煤气使用量/m3 | 煤气费/元 |
| 7月 | 4 | 4 |
| 8月 | 25 | 14 |
| 9月 | 35 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com