
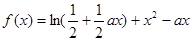 。(
。(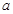 为常数,
为常数,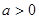 )
)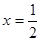 是函数
是函数 的一个极值点,求
的一个极值点,求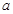 的值;
的值;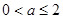 时,
时, 在
在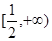 上是增函数;
上是增函数;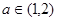 ,总存在
,总存在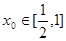 ,使不等式
,使不等式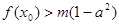 成立,求实数
成立,求实数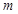 的取值范围。
的取值范围。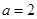 ;(Ⅱ)详见解析;(Ⅲ)实数
;(Ⅱ)详见解析;(Ⅲ)实数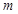 的取值范围为
的取值范围为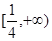
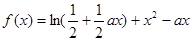 ,
,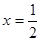 是函数
是函数 的一个极值点,先求出其导函数:
的一个极值点,先求出其导函数: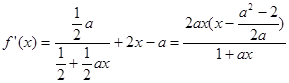 ,利用
,利用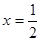 是函数
是函数 的一个极值点对应的结论,即
的一个极值点对应的结论,即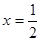 时,它的导函数值为零,可令
时,它的导函数值为零,可令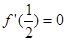 ,即可求
,即可求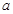 的值;(Ⅱ)求证:当
的值;(Ⅱ)求证:当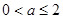 时,
时, 在
在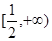 上是增函数,由于
上是增函数,由于 含有对数函数,可通过求导来证明,因此利用:
含有对数函数,可通过求导来证明,因此利用: ,在
,在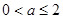 时,分析出因式中的每一项都大于等于0,即得
时,分析出因式中的每一项都大于等于0,即得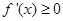 ,从而可证明结论;(Ⅲ)先由(Ⅱ)知,
,从而可证明结论;(Ⅲ)先由(Ⅱ)知, 在
在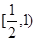 上的最大值为
上的最大值为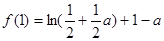 ,把问题转化为对任意的
,把问题转化为对任意的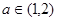 ,不等式
,不等式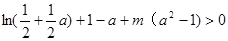 恒成立;然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数
恒成立;然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数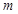 的取值范围为
的取值范围为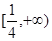 .
.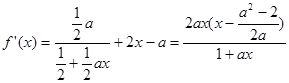
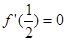 且
且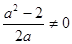 ,
,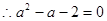

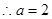 3分
3分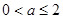 时,
时,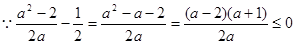
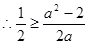
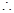 当
当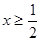 时,
时,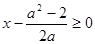 又
又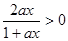
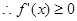
 在
在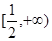 上是增函数 6分
上是增函数 6分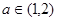 时,由(Ⅱ)知,
时,由(Ⅱ)知, 在
在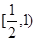 上的最大值为
上的最大值为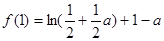
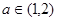 ,不等式
,不等式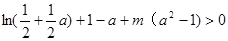 恒成立。
恒成立。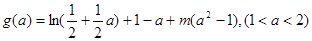
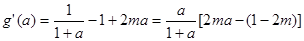
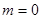 时,
时,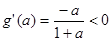
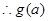 在区间
在区间 上递减,此时
上递减,此时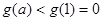
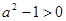 ,
,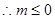 时不可能使
时不可能使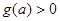 恒成立,故必有
恒成立,故必有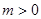
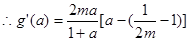
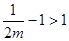 ,可知
,可知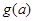 在区间
在区间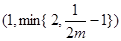 上递减,在此区间上,有
上递减,在此区间上,有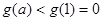 ,与
,与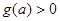 恒成立相矛盾,故
恒成立相矛盾,故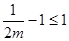 ,这时
,这时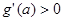 ,
,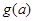 在
在 上递增,恒有
上递增,恒有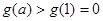 ,满足题设要求,
,满足题设要求,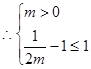 即
即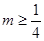
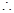 实数
实数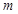 的取值范围为
的取值范围为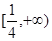 14分
14分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
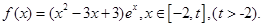
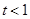 时,求函数
时,求函数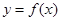 的单调区间;
的单调区间;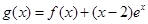 ,试问函数
,试问函数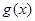 在
在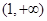 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com