练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC的中点.则下列结论中不正确的是　　　　. 

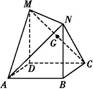
    ①MC⊥AN

    ②GB∥平面AMN

    ③平面CMN⊥平面AMN

    ④平面DCM∥平面ABN


    ③解析:显然该几何图形为正方体截去两个三棱锥所剩的几何体,把该几何体放置到正方体中(如图),作AN的中点H,连接HB,MH,GB,则MC∥HB,又HB⊥AN,所以MC⊥AN,所以①正确;由题意易得GB∥MH,又GB⊄平面AMN,MH⊂平面AMN,所以GB∥平面AMN,所以②正确;因为AB∥CD,DM∥BN,且AB∩BN=B,CD∩DM=D,所以平面DCM∥平面ABN,所以④正确.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若0＜x＜1，则f(x)＝x(4－3x)取得最大值时，x的值为 (　　)

    A.            B.             C.              D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A、B、C、D是空间中四个不同的点,下列命题中,不正确的是(　)

    (A)若AC与BD共面,则AD与BC共面

    (B)若AC与BD是异面直线,则AD与BC是异面直线

    (C)若AB=AC,DB=DC,则AD=BC

    (D)若AB=AC,DB=DC,则AD⊥BC

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设平面α∥平面β,A∈α,B∈β,C是AB的中点,当A、B分别在α、β内移动时,那么所有的动点C(　　)

    (A)不共面

    (B)当且仅当A、B在两条相交直线上移动时才共面

    (C)当且仅当A、B在两条给定的平行直线上移动时才共面

    (D)不论A、B如何移动都共面

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正四棱柱ABCDA1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,则点Q满足条件　　　　时,有平面D1BQ∥平面PAO. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD,则在三棱锥ABCD中,下列结论正确的是(　　)

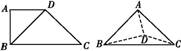
    (A)平面ABD⊥平面ABC    (B)平面ADC⊥平面BDC

    (C)平面ABC⊥平面BDC    (D)平面ADC⊥平面ABC

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a、b、l表示三条不同的直线,α、β、γ表示三个不同的平面,有下列四个命题:

    ①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;

    ②若a、b相交,且都在α、β外,a∥α,a∥β,b∥α,b∥β,则α∥β;

    ③若α⊥β,α∩β=a,b⊂β,a⊥b,则b⊥α;

    ④若a⊂α,b⊂α,l⊥a,l⊥b,l⊄α,则l⊥α.

    其中正确命题的序号是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直三棱柱ABCA′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.

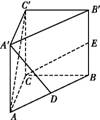
    (1)求证:CE⊥A′D;

    (2)求异面直线CE与AC′所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用演绎法证明“函数y＝x3是增函数”时的大前提是(　　)

    A．增函数的定义 

    B．函数y＝x3满足增函数的定义

    C．若x1<x2，则f(x1)<f(x2) 

    D．若x1>x2，则f(x1)>f(x2)

    查看答案和解析>>

    同步练习册答案