
分析 (1)求出函数的导数,得到关于a,b的方程组,求出f(x)的解析式,设T(x)=f(x)-2x-2m=lnx-x-2m,根据函数的单调性求出a的范围即可;
(2)求出F(x)的导数,等价于方程x2-2x+m=0在(0,+∞)内有2个不等实根,根据函数的单调性证明结论即可.
解答 解:(1)∵f′(x)=1+$\frac{a}{x}$,g′(x)=$\frac{b}{{x}^{2}}$,
根据题意得$\left\{\begin{array}{l}{1+a=b}\\{1=3-b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$;
∴f(x)=x+lnx,
设T(x)=f(x)-2x-2m=lnx-x-2m,则T′(x)=$\frac{1}{x}$-1,
当x∈(0,1)时,T′(x)>0,当x∈(1,+∞)时,T′(x)<0,
∴T(x)max=T(1)=-1-2m,
∵x→0时,T(x)→-∞,
x→+∞时,T(x)→-∞,
故要使两图象有2个交点,只需-1-2a>0,解得:a<-$\frac{1}{2}$,
故实数a的范围是(-∞,-$\frac{1}{2}$);
(2)证明:由题意,函数F(x)=x-$\frac{m}{x}$-2lnx,其定义域是(0,+∞),
F′(x)=$\frac{{x}^{2}-2x+m}{{x}^{2}}$,
令F′(x)=0,即x2-2x+m=0,其判别式△=4-4m,
函数F(x)有2个极值点x1,x2,
等价于方程x2-2x+m=0在(0,+∞)内有2个不等实根,
又x1x2>0,故0<m<1,
∴x2=1+$\sqrt{1-m}$且1<x2<2,m=-${{x}_{2}}^{2}$+2x2,
F (x2)-x2+1=x2-2lnx2-1,
令h(t)=t-2lnt-1,1<t<2,
则h′(t)=$\frac{t-2}{t}$,
由于1<t<2,则h′(t)<0,
故h(t)在(1,2)递减,
故h(t)<h(1)=1-2ln1-1=0,
∴F(x2)-x2+1=h(x2)<0,
∴F(x2)<x2-1.
点评 本题考查导数的几何意义,利用导数研究函数的单调性、最值研究不等式恒成立问题,考查运算求解能力、函数与方程思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48里 | B. | 24里 | C. | 12里 | D. | 6里 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
| A. | 4.5 | B. | 4.6 | C. | 4.7 | D. | 4.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
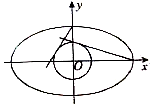 如图,过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>1)上顶点和右顶点分别作圆x2+y2=1的两条切线的斜率之积为-$\frac{{\sqrt{2}}}{2}$,则椭圆的离心率的取值范围是$({0,\frac{{\sqrt{2}}}{2}})$.
如图,过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>1)上顶点和右顶点分别作圆x2+y2=1的两条切线的斜率之积为-$\frac{{\sqrt{2}}}{2}$,则椭圆的离心率的取值范围是$({0,\frac{{\sqrt{2}}}{2}})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,1) | C. | (2,2) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com