Question

已知数列{a_n}的前n项和为S_n，若S₁=1，S₂=2，且S_n+1-3S_n+2S_n-1=0（n∈N^*且n≥2），求该数列的通项公式．

Answer 1

解：由S₁=1得a₁=1，又由S₂=2可知a₂=1．
∵S_n+1-3S_n+2S_n-1=0（n∈N^*且n≥2），
∴S_n+1-S_n-2S_n+2S_n-1=0（n∈N^*且n≥2），
即（S_n+1-S_n）-2（S_n-S_n-1）=0（n∈N^*且n≥2），
∴a_n+1=2a_n（n∈N^*且n≥2），故数列{a_n}从第2项起是以2为公比的等比数列．
∴数列{a_n}的通项公式为a_n=
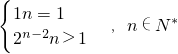
分析：求的是数列的通项公式条件是数列{a_n}的前n项和为S_n，由所以由两者间的关系求解．要注意分类讨论．
点评：本题主要考查数列的前n项和通项公式及两者间的关系的应用．