
若关于 的不等式
的不等式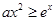 的解集中的正整数解有且只有3个,则实数
的解集中的正整数解有且只有3个,则实数 的取值范围是 .
的取值范围是 .
科目:高中数学 来源: 题型:填空题
函数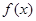 的导函数为
的导函数为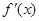 ,若对于定义域内任意
,若对于定义域内任意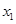 ,
,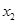
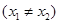 ,有
,有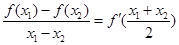 恒成立,则称
恒成立,则称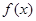 为恒均变函数.给出下列函数:①
为恒均变函数.给出下列函数:①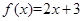 ;②
;②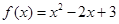 ;③
;③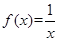 ;④
;④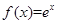 ;⑤
;⑤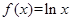 .其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
.其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
A、B两地相距1千米,B、C两地相距3千米,甲从A地出发,经过B前往C地,乙同时从B地出发,前往C地.甲、乙的速度关于时间的关系式分别为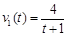 和
和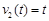 (单位:千米/小时).甲、乙从起点到终点的过程中,给出下列描述:
(单位:千米/小时).甲、乙从起点到终点的过程中,给出下列描述:
①出发后1小时,甲还没追上乙 ② 出发后1小时,甲乙相距最远
③甲追上乙后,又被乙追上,乙先到达C地 ④甲追上乙后,先到达C地
其中正确的是 .(请填上所有描述正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知函数y=f(x)是定义在R上的奇函数,且当x>0时,f(x)+xf′(x)>0(其中f′(x)是f(x)的导函数),设a=(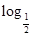 4)f(
4)f(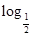 4),b=
4),b=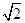 f(
f(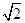 ),c=(lg
),c=(lg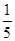 )f(lg
)f(lg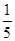 ),则a,b,c由大到小的关系是________.
),则a,b,c由大到小的关系是________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
我们把形如y=f(x)φ(x)的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得ln y=φ(x)lnf(x),两边求导得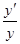 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)·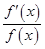 ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·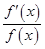 ].运用此方法可以探求得y=x
].运用此方法可以探求得y=x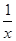 的单调递增区间是________.
的单调递增区间是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com