练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示：用篱笆围成一个一边靠墙的矩形菜园 ，假设墙有足够长．

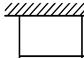
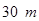    (Ⅰ) 若篱笆的总长为，则这个矩形的长，宽各为多少时，菜园的面积最大？
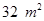    (Ⅱ) 若菜园的面积为，则这个矩形的长，宽各为多少时，篱笆的总长最短？
    (Ⅰ) 矩形的长为，宽为时，菜园的面积最大 (Ⅱ) 矩形的长为、宽为时，可使篱笆的总长最短

    试题分析：设这个矩形的长为，宽为，篱笆的长为，面积为．
    (Ⅰ) 由题知，由于，
    ∴，，即，当且仅当时等号成立．
    由
    故这个矩形的长为，宽为时，菜园的面积最大．
    (Ⅱ) 条件知，.
    ,当且仅当时等号成立．
    由 
    故这个矩形的长为、宽为时，可使篱笆的总长最短．
    点评：利用均值不等式求最值时要注意其满足的三个条件：一，都是正数，二，积为定值时和取得最值，和为定值时积为定值，三，等号成立的条件看是否满足
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    在矩形中，，，现截去一个角，使分别落在边上，且的周长为8，设，,则用表示的表达式为      ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    矩形ABCD中，轴，且矩形ABCD恰好能完全覆盖函数的一个完整周期图象，则当变化时，矩形ABCD周长的最小值为       .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知，则的最大值为                。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (9分）设x>0,y>0且x+y=1，求证：≥9.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若，则的最小值为____________. 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


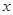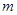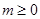    为了提高产品的年产量，某企业拟在2013年进行技术改革．经调查测算，产品当年的产量万件与投入技术改革费用万元（）满足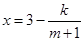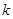（为常数）．如果不搞技术改革，则该产品当年的产量只能是1万件．已知2013年生产该产品的固定收入为8万元，每生产1万件该产品需要再投入16万元．由于市场行情较好，厂家生产的产品均能销售出去．厂家将每件产品的销售价格定为每件产品生产成本的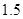倍（生产成本包括固定投入和再投入两部分资金）．
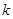    （Ⅰ）试确定的值，并将2013年该产品的利润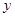万元表示为技术改革费用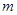万元的函数（利润=销售金额­―生产成本―技术改革费用）；
    （Ⅱ）该企业2013年的技术改革费用投入多少万元时，厂家的利润最大？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知正数x, y满足x+2y=1,则的最小值是         .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若正数满足，则的最大值为         .

    查看答案和解析>>

    同步练习册答案