
| A. | b=10,A=45°,B=60° | B. | a=60,c=48,B=120° | ||
| C. | a=7,b=5,A=75° | D. | a=14,b=16,A=45° |
分析 由条件利用正弦定理、余弦定理以及大边对大角,判断△ABC解的个数.
解答 解:若b=10,A=45°,B=60°,则由正弦定理可得$\frac{a}{sin45°}$=$\frac{10}{sin60°}$,求得a=$\frac{10\sqrt{6}}{3}$,故△ABC有一解;
若a=60,c=48,B=120°,则由余弦定理可得b2=a2+c2-2ac•cosB=8784,求得b只有一解,故△ABC有一解;
若a=7,b=5,A=75°,则由正弦定理可得$\frac{7}{sin75°}$=$\frac{5}{sinB}$,求得sinB=$\frac{28}{\sqrt{6}+\sqrt{2}}$,
再根据b<a,可得B为锐角,故角B只有一个,故△ABC有一解;
若a=14,b=16,A=45°,则由正弦定理可得 $\frac{14}{sin45°}$=$\frac{16}{sinB}$,求得sinB=$\frac{4\sqrt{2}}{7}$,
再根据b>a,可得B>A,∴B可能是锐角也可能是钝角,即角B有2个值,故△ABC有两解,
故选:D.
点评 本题主要考查正弦定理、余弦定理的应用,大边对大角,属于基础题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
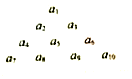 在等差数列{an}中,已知a3=7,a6=16,将此等差数列的各项排成如图所示的三角形数阵,则此数阵中,第10行从左到右的第5个数是148.
在等差数列{an}中,已知a3=7,a6=16,将此等差数列的各项排成如图所示的三角形数阵,则此数阵中,第10行从左到右的第5个数是148.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com