
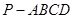 中,底面
中,底面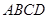 为直角梯形,
为直角梯形,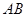 ∥
∥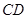 ,
, 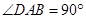 ,
,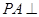 平面
平面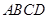 ,且
,且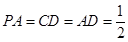 ,
,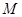 为
为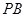 的中点
的中点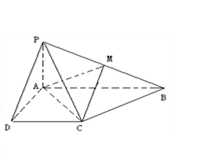
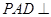 面
面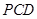
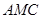 与面
与面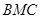 夹角的余弦值.
夹角的余弦值.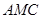 与面
与面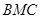 夹角的余弦值
夹角的余弦值 .
.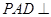 面
面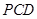 ,在立体几何中,证明面面垂直,往往转化为证明线面垂直,即证一个平面过另一个平面的垂线,由已知
,在立体几何中,证明面面垂直,往往转化为证明线面垂直,即证一个平面过另一个平面的垂线,由已知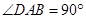 ,即
,即 ,又因为
,又因为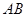 ∥
∥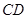 ,则
,则 ,只需在平面
,只需在平面 内再找一条垂线即可,由已知
内再找一条垂线即可,由已知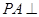 平面
平面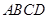 ,从而得
,从而得 ,这样
,这样 平面
平面 ,即得面
,即得面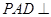 面
面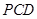 ;也可利用向量法, 以
;也可利用向量法, 以 为坐标原点
为坐标原点 长为单位长度,分别以
长为单位长度,分别以 为
为 轴建立空间直角坐标系,利用向量来证
轴建立空间直角坐标系,利用向量来证 ,即得
,即得 ,其它同上;
,其它同上;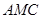 与面
与面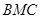 夹角的余弦值,可建立空间直角坐标系,利用向量法求二面角的大小,由(1) 建立的间直角坐标系,设出两个半平面的法向量,利用法向量的性质,求出两个半平面的法向量,利用法向量来求平面
夹角的余弦值,可建立空间直角坐标系,利用向量法求二面角的大小,由(1) 建立的间直角坐标系,设出两个半平面的法向量,利用法向量的性质,求出两个半平面的法向量,利用法向量来求平面 与平面
与平面 的夹角的余弦值.
的夹角的余弦值. 为坐标原点
为坐标原点 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为 .
.

 ,且
,且 与
与 是平面
是平面 内的两条相交直线,由此得
内的两条相交直线,由此得 面
面 .
. 在面
在面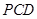 上,故面
上,故面 ⊥面
⊥面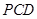 . 5分
. 5分 上取一点
上取一点 ,则存在
,则存在 使
使

 ,只需
,只需 ,即
,即 ,解得
,解得 ,可知当
,可知当 时,
时, 点的坐标为
点的坐标为 ,能使
,能使 ,此时
,此时 ,
, ,有
,有 ,由
,由 得
得 ,所以
,所以 为所求二面角的平面角.因为
为所求二面角的平面角.因为 ,
, ,
, ,故
,故 .
.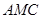 与面
与面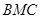 夹角的余弦值
夹角的余弦值 . 12分
. 12分

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
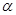 ,
,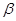 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定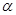 ∥
∥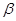 的是( )
的是( )A.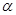 , ,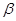 都与平面 都与平面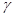 垂直 垂直 |
B.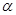 内不共线的三点到 内不共线的三点到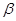 的距离相等 的距离相等 |
C.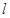 , ,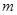 是 是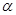 内的两条直线且 内的两条直线且 ∥ ∥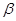 , ,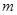 ∥ ∥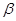 |
D.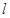 , ,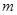 是两条异面直线且 是两条异面直线且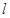 ∥ ∥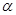 , ,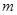 ∥ ∥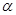 , , ∥ ∥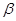 , , 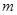 ∥ ∥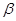 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com