
| A. | 等腰三角形 | B. | 正三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
分析 由$\overrightarrow{BP}=\overrightarrow{PC}$,得到P为BC中点,结合$\overrightarrow{AP}•\overrightarrow{AB}$=$\overrightarrow{AP}•\overrightarrow{AC}$,变形得到AP⊥BC,即AP是BC的垂直平分线,所以AB=AC.
解答 解:因为$\overrightarrow{BP}=\overrightarrow{PC}$,所以BP=PC,
又$\overrightarrow{AP}•\overrightarrow{AB}$=$\overrightarrow{AP}•\overrightarrow{AC}$,
所以$\overrightarrow{AP}•(\overrightarrow{AB}-\overrightarrow{AC})$=0,
即$\overrightarrow{AP}•\overrightarrow{CB}$=0,
所以$\overrightarrow{AP}⊥\overrightarrow{BC}$,
所以AB=AC;
故选A.
点评 本题考查了平面向量的运用;通过向量相等包括方向相同、长度相等;数量积为0,得到向量垂直.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\root{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-1或a>3 | B. | -1<a<3 | C. | -1<a<2 | D. | 1<a<3 |
查看答案和解析>>
科目:高中数学 来源:2017届江西南昌新课标高三一轮复习训练三数学试卷(解析版) 题型:选择题
已知函数 则下列结论正确的是( )
则下列结论正确的是( )
A. 是偶函数 B.
是偶函数 B. 是增函数
是增函数
C.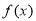 是周期函数 D.
是周期函数 D. 的值域为
的值域为
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(文)试卷(解析版) 题型:填空题
已知函数 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,令
对称,令 ,则关于函数
,则关于函数 有下列命题:
有下列命题:
① 的图象关于原点对称;
的图象关于原点对称;
② 为偶函数;
为偶函数;
③ 的最小值为0;
的最小值为0;
④ 在
在 上为减函数.
上为减函数.
其中正确命题的序号为____________.(注:将所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com