
 如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.
如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$. 分析 设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,(a>b>0),由题意求出a,b,c,由此能求出该椭圆的离心率.
解答 解:不妨设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,(a>b>0),
由题意得$\left\{\begin{array}{l}{2a=2a-4}\\{b=2}\end{array}\right.$,
解得a=8,b=2,c=$\sqrt{64-4}$=2$\sqrt{15}$,
∴该椭圆的离心率为e=$\frac{c}{a}$=$\frac{2\sqrt{15}}{8}$=$\frac{\sqrt{15}}{4}$.
故答案为$\frac{\sqrt{15}}{4}$.
点评 本题考查椭圆的离心率的求法,解题时要认真审题,注意椭圆性质的合理运用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin3-cos3 | B. | sin3-cos3 | C. | sin3+cos3 | D. | cos3-sin3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
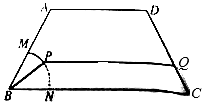 如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.
如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{60}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com